Bonjour,
Je dois démontrer quune sigma-algèbre M sur E un ensemble non vide est bien une algèbre au sens classique du terme.
Soit la loi V telle que pour A et B de M, AVB soit lensemble des éléments de E appartenant exactement à A ou B, il sagit dabord de démontrer que M est un groupe relativement à V.
Jai déjà démontré que AM et BM => A inter B M (désolée pour les notations
) et donc que AVB M.
Jallais continuer la démonstration en considérant que lélément neutre pour la loi V était lensemble vide
ce qui apparemment est faux, et ça me surprend beaucoup. Quel est lélément neutre alors ?
(Le prof donne comme indication que AVB est lunion de lintersection de A et du complémentaire de B dans E, et de lintersection de B et du complémentaire de A dans E.)
Sigma-algèbre
5 messages
- Page 1 sur 1
Si vraiment 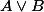 est la différence symétrique de
est la différence symétrique de  et
et  ,alors :
,alors :
 \cup (B-A)) , si bien que pour tout
, si bien que pour tout  :
:
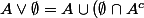 = A = \emptyset \vee A)
Donc si la loi est vraiment définie comme dans ton énoncé (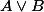 est l'ensemble des éléments qui sont soit dans A sans être dans B, soit dans B sans être dans A), tu n'as pas le choix, il doit y avoir un malentendu avec ta prof.
est l'ensemble des éléments qui sont soit dans A sans être dans B, soit dans B sans être dans A), tu n'as pas le choix, il doit y avoir un malentendu avec ta prof.
Donc si la loi est vraiment définie comme dans ton énoncé (
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
