Sur les nombres complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 04 Nov 2011, 14:09
par Epsilon » 04 Nov 2011, 14:09
Bonjour à tous
alors un petit soucis dans cet exercice
Le problème et de déterminer les

tel que les image de

, et
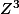
sont alignés.
Alors puisque on parle de l'alignement donc je travaille avec un

de la forme :

, de même

et
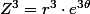
Image alignées

et aprés ??? je ne sais pas quoi faire !!
merci d'avance pour votre aide.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2011, 14:18
par arnaud32 » 04 Nov 2011, 14:18
modulo 2*pi ou modulo pi ?
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 04 Nov 2011, 20:44
par Epsilon » 04 Nov 2011, 20:44
sur la même droite . oui c'est vrai modulo pi
mais bon mon problème est le même !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 04 Nov 2011, 20:47
par arnaud32 » 04 Nov 2011, 20:47
Écris les 3 équations et fait des recoupements
a=2a[pi] ssi a=0[pi] ...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 04 Nov 2011, 21:08
par Doraki » 04 Nov 2011, 21:08
Epsilon a écrit:Image alignées

euh c'est loin d'être suffisant. Il y a des droites qui ne passent pas par l'origine.
Par exemple il me semble bien que les points d'affixe (1-i), 1, et (1+i) sont alignés, tandis que leurs arguments, -pi/4, 0, et pi/4, ne sont pas égaux modulo 2pi.
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 04 Nov 2011, 21:20
par Epsilon » 04 Nov 2011, 21:20
ok
donc
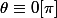
et
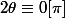
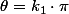
et
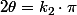
avec
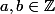
la formule qui englobe les deux cas c'est bien la première c'est à dire un

de la forme : un truc relatif multiplié par

non ?
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 04 Nov 2011, 21:22
par Epsilon » 04 Nov 2011, 21:22
Doraki a écrit:euh c'est loin d'être suffisant. Il y a des droites qui ne passent pas par l'origine.
Par exemple il me semble bien que les points d'affixe (1-i), 1, et (1+i) sont alignés, tandis que leurs arguments, -pi/4, 0, et pi/4, ne sont pas égaux modulo 2pi.
donc sa change tous ! tous mon raisonnement est faux !!
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 04 Nov 2011, 21:26
par Bony » 04 Nov 2011, 21:26
Il faut travailler sur l'argument de z,z² et z^3.
En effet, si ces 3 points sont alignés alors arg((z^3-z)/(z²-z)) est nul modulo pi.
Tu peux simplifier par z en le supposant non nul (sans quoi l'argument n'aurait pas de sens), Pour le cas z=1 c'est en effet vrai car les points d'affixe z, z² et z^3 sont bien alignés. De même pour -1. Si z =/ 1,-1 alors
Arg((z²-1)/(z-1)) est nul modulo pi, auquel cas Arg(z+1) est nul modulo pi.
Tu peux écrire z = x+iy, soit Arg(x+iy+1) nul modulo pi, soit encore y nul.
-
Epsilon
- Membre Relatif
- Messages: 175
- Enregistré le: 08 Nov 2006, 14:23
-
 par Epsilon » 04 Nov 2011, 21:34
par Epsilon » 04 Nov 2011, 21:34
merci bony
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités