DM 3ème

[Ahleks]

Bonjour,

Quelqu'un pourrais m'aider pour mon DM de math je suis en 3ème, je vous donne les deux premières questions :

1) Développer et réduire les expressions suivantes: G= (3x -5)² H= (9x +1)(9x -1)

J'ai trouvé:

G= (3x-5)²
G= 3x² + 2 × 3x × (-5) + 5²
G= 3x + (-3) × 3x + 5²

H= (9x +1)(9x -1)
H= 9x × 9x - 9x × 1 + 1 × 9x - 1 × 1
H= 81x - 9x + 9x - 1
H= 81x - 1

2) Utiliser une identité remarquable pour calculer à la main 10 007²

Par contre là j'ai rien trouvé du tout --"

Comme je suis un peu nulle :dodo: , j'aimerais savoir si quelqu'un pourrais déjà me corriger ces deux question et je mettrais les autres ensuite :)
Merci d'avance :happy3:

[titine]

Bonjour,

Quelqu'un pourrais m'aider pour mon DM de math je suis en 3ème, je vous donne les deux premières questions :

1) Développer et réduire les expressions suivantes: G= (3x -5)² H= (9x +1)(9x -1)

J'ai trouvé:

G= (3x-5)²
G= (3x)² + 2 × 3x × (-5) + 5²
G= 9x² + (-10) × 3x + 5²

C= 9x² - 30x + 25

H= (9x +1)(9x -1)
H= 9x × 9x - 9x × 1 + 1 × 9x - 1 × 1
H= 81x² - 9x + 9x - 1
H= 81x² - 1

Mais tu aurais pu reconnaitre A+B)(A-B) = A² - B²
Donc (9x+1)(9x-1) = (9x)² - 1² = 81x² - 1

2) Utiliser une identité remarquable pour calculer à la main 10 007²

10 007² = (10 000 + 7)² = 10 000² + 2*10 000*7 + 7² = 100000000 + 140000 + 49 = 100140049

[Adoration_For_None]

Bonjour,

1)
En développant tu trouves
Attention ton identité remarquable c'est , le carré porte sur tout le nombre a, ici 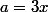donc ce n'est pas 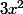, mais .
Ainsi quand tu calcules, ce que tu as oublié de faire, tu obtiens .


Ton résultat est juste à un carré prêt et non , mais quoi qu'il en soit tu aurais dû identifier l'identité remarquable suivante , de cette façon le résultat tombe immédiatement.

2) Tu dois calculer 10 007², tu remarques donc que 10 007=10 000+7. Ainsi 10 007²=(10 000+7)². Et tu as une identité remarquable de la forme .
Ainsi 10 007² = 10 000²+10 000x7x2+7².
Une puissance de 10 (=1, 10, 100, ...) quand elle est mise au carré ça revient à doubler le nombre de zéro.
Ainsi tu as 10 007²=100 000 000+140 000+49=100 140 049.

Je te rappelle les identités remarquables pour la suite des exercices :

[Adoration_For_None]

C= 9x² - 30x + 25


Mais tu aurais pu reconnaitre A+B)(A-B) = A² - B²
Donc (9x+1)(9x-1) = (9x)² - 1² = 81x² - 1

10 007² = (10 000 + 7)² = 10 000² + 2*10 000*7 + 7² = 100000000 + 140000 + 49 = 100140049

Plus rapide que moi.

[titine]

Attention on a
(A + B) = A² + 2AB + B²
Donc lorsqu' on a (3x + 5)²
A est égal à 3x
Donc A² c'est (3x)² c'est à dire (3x)*(3x) = 9x²

[Ahleks]

Merci Adoration et titine :lol3:

Ensuite, pour l'exercice 2 j'ai:

Donner l'écriture décimale de ces 3 nombres en écrivant toutes les étapes de calcul.

B= 6²+3²*9
C= 2(exposant3) / 12+2²
D= 5x10 (exposant3) -2x10²

Donc, si je me rappelle bien, les écritures décimales, c'est quand on peut écrire des nombres avec des virgules, or, dans les trois, je ne trouve qu'un nombre à virgule :cry:

J'ai fait:

B= 6²+3²*9
B= 36+9*9
B=36+81
B= 117

C= 2(exposant3) / 12+2²
C= 8/12+4
C=8/16
C=0.5

D= 5x10 (exposant3) -2x10²
D= 5*1000-2*100
D= 5000-200
D= 4800

[Adoration_For_None]

Tes calculs sont parfaitement juste.
Une écriture décimale de a c'est . Les nombres décimaux c'est tous les nombres que tu peux écrire avec une fraction de 1,10,100.
Donc pour 117 tu mets , pour 0.5 : et pour 4800 . C'est très intelligent je l'avoue

[Ahleks]

Re bonjour,

J'ai complétement oublié mon DM :doh:

Merci adoration, c'est tout bête en faite :ptdr:

Alors pour l'exercice 4 on nous dit:
Soit l'expression littérale suivante: L= 7x² - 5x + 12

Calculer L pour x = -6

J'ai fait :
L= 7x² - 5x + 12
L= 7 * 36 - 5x + 12
L= 7 * 36 - 5x + 12
L= 252 - 5x + 12
L= 264 - 5x

Est-ce que c'est bon ?

[Adoration_For_None]

Et rajoute

L=264-5*-6
L=294

Et c'est bon. :)

[Ahleks]

C'est fait :)

Pour l'exercice 5:

On considère la figure si dessous telle que M, A, P et I soient 4 points du cercle de diamètre [AI];
On donne: AI=8 cm AM=6.5cm PÂI = 42°

(Désolée je sais pas comment mettre une figure)

1) Prouver que AMI est un triangle rectangle

J'ai fait :

On sait que AMI est un triangle qui est inscrit dans le cercle et a pour côté un diamètre de ce cercle.
Or, si un triangle est inscrit dans un cercle et a pour côté un diamètre de ce triangle, alors ce triangle est rectangle.

2) Calculer la longueur MI, donner la valeur exacte puis la valeur arrondie au mm.

MI² = IA² - MA²
MI²= 8² - 6.5²
MI= 64 - 42.25
MI= Racine carré de 21.75
MI = 4.663689527

Donc, MI à peu près egal à 4.7cm

3) Calculer la longueur PI, donner la valeur exacte puis la valeur arrondie au mm.

Là j'ai pas comprit quoi utiliser pour trouver la longueur.