Suites par récurrence.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Colorado1
- Messages: 2
- Enregistré le: 31 Oct 2011, 14:36
-
 par Colorado1 » 31 Oct 2011, 14:46
par Colorado1 » 31 Oct 2011, 14:46
On définit la suite (U ) n;)1 par U
) n;)1 par U =1 et pour tout n;)1, U
=1 et pour tout n;)1, U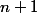 = 2U
= 2U + 1.1. Calculer U
+ 1.1. Calculer U , U
, U , U
, U , U
, U , U
, U .
.
2. Démontrer par récurrence que pour tout n;)1, U =
=  - 1.
- 1.1. Mes résultats sont: U

=4, U

=10, U

=22, U

=46, U

=98.
2. J'ai ceci:
Montrons que pour n;)1, U

=

-1.
Initialisation:Pour n=1, a-t'on U

=
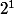
- 1 ?
U
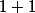
=
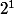
- 1 = 1 donc U

=

- 1 est vraie.
Hérédité:Supposons que pour un entier k;)1, on ait U

=
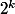
- 1.
Montrons que cette propriété est vraie pour k+1, soit U
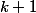
=
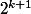
- 1.
U
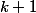
=
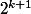
- 1
Voilà, après je suis un peu perdue... quelqu'un peut-il m'aider?
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 31 Oct 2011, 17:05
par gigamesh » 31 Oct 2011, 17:05
Colorado1 a écrit:On définit la suite (U ) n;)1 par U
) n;)1 par U =1 et pour tout n;)1, U
=1 et pour tout n;)1, U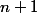 = 2U
= 2U + 1.1. Calculer U
+ 1.1. Calculer U , U
, U , U
, U , U
, U , U
, U .
.
2. Démontrer par récurrence que pour tout n;)1, U =
=  - 1.
- 1.1. Mes résultats sont: U

=4, U

=10, U

=22, U

=46, U

=98.
2. J'ai ceci:
Montrons que pour n;)1, U

=

-1.
Initialisation:Pour n=1, a-t'on U

=
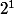
- 1 ?
U
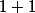
=
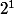
- 1 = 1 donc U

=

- 1 est vraie.
Hérédité:Supposons que pour un entier k;)1, on ait U

=
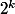
- 1.
Montrons que cette propriété est vraie pour k+1, soit U
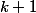
=
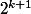
- 1.
U
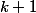
=
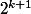
- 1
Voilà, après je suis un peu perdue... quelqu'un peut-il m'aider?
Salut,
le calcul de
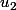
est incorrect.
De
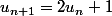
on déduit, en remplaçant n par 1,
que
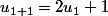
donc
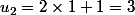
Refais les calculs correctement pour la question 1, avant d'attaquer la récurrence.
-
Colorado1
- Messages: 2
- Enregistré le: 31 Oct 2011, 14:36
-
 par Colorado1 » 02 Nov 2011, 13:26
par Colorado1 » 02 Nov 2011, 13:26
Merci, j'ai rectifié:
U2=3, U3=7, U4=15, U5=31, U6=63
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 02 Nov 2011, 14:26
par Teacher » 02 Nov 2011, 14:26
C'est correct !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
