Exercice d'intégration

[beuj]

Bonjour à tous,
J'ai des exercices sur les intégrales qui sont un peu corsés... j'aimerais un coup de main pour me lancer sur le chemin de la solution!

Ex1
Soit f une fonction continue sur [a;b] tel que ;) x ;) [a;b] , f(x)=f(a+b-x)

1) montrer que l'on à l'intégrale de a à b (x f(x) dx) = (a+b/2) intégrale de a à b (f(x) dx)

2) en déduire la valeur de intégrale de 0 à pi (x sinx / 1+cos^2 x) dx)

pour le 1) j'ai exprimé les intégrales en fonction de a et b. Pour celle de gauche, avec une intégration par partie j'obtiens F(b)(b-1)+F(a)(a+1) ; F étant une primitive de f. Pour celle de gauche : ((a+b)/2)(F(b)-F(a)). Et quand je remplace f(x) par f(a+b-x) j'arrive encore à des résultats différents... Pour la 2) j'ai identifié a=0, b=pi, x=x :lol5: et f(x)=sin x / (1+cos^2 x). J'ai calculé l'intégrale par changement de variable en posant t=cos x et je trouve -(pi^2) /4... je suis pas convaincu... :look2:

Ex2
on considère l'intégrale In = intégrale de 0 à 1 (x^n V(1-x) dx) -> x puissance n * racine de (1-x)!
, n ;) N
1) etablir pour n>1 une relation entre In et In-1
2) calculer In

... aucun début d'inspiration...
Merci pour votre aide!

[mathelot]

pour la (2) , intégrer par parties en puissance

[beuj]

Merci pour ton aide, mais ce serait plutôt puissance 1/2 pour oter la racine, non?

[beuj]

j'ai rien dit.... je l'ai la puissance 3/2! :id:
merci.

[mathelot]

pour la 1.1
le changement de variable
permet de parcourir le segment [a;b] en décroissant
-du= dx
...

pour la (2) le changement de variable proposé en 1.1 permet de se ramener
à qui se primitive avec un arctan

[beuj]

Bonjour Mathelot,
Pour le changement de variable, je ne vois pas trop où tu veux en venir :
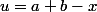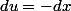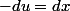si je pose , j'ai donc , ok.
Les bornes de l'intégrale deviennent : si x=a, u=b et si x=b, u=a. De plus j'ai x=a+b-u. Mon intégrale devient : . Je ne vois pas ce qu'apporte le changement de variable.
Pour la 1.2, je pense que ce que tu me suggères équivaut à ce j'ai dis : En posant , j'ai . Les bornes devienent 1 pour x=0 et -1 pour x=. L'intégrale devient (en s'aidant de l'égalité que je n'arrive pas à démontrer) : = : = (et non , j'ai trouvé mon erreur.) le résultat me convient mieux! :lol3:
Pour le 2.1, toujours pas de résultat! Et pour le 2.2, merci du coup de main, c'était tout con en fait!

[Bony]

Si tu note tu ne trouverais pas par hasard que

[beuj]

merci pour vos indications! Si je ne me suis pas planter dans le développement de ; je retombe bien sur l'égalité de départ.
Merci à tous les deux!

[beuj]

Par contre, pour l' ex2, quand je calcule , j'arrive à :
je suis pas loin d'avoir en fonction de à la puissance près... si quelqu'un à un tuyau...

[beuj]

Je me suis encore planté... :mur: ... j'ai trouvé ma relation entre et ...