comment montre t-on que pour une fonction continue f on a :
Limite intégrale
6 messages
- Page 1 sur 1
limite intégrale
par lisonn » 29 Oct 2011, 16:54
Bonjour,
comment montre t-on que pour une fonction continue f on a :}dx) -> \max_{a<x<b} f(x))
quant t tends vers l'infini ?
comment montre t-on que pour une fonction continue f on a :
par girdav » 29 Oct 2011, 17:17
Il doit manquer un 
quelque part dans le membre de gauche, en l'état ça tend vers 
.
par girdav » 29 Oct 2011, 18:03
On a que }dx\)\leq \max_{a\leq x\leq b}f(x)=:M)
. Maintenant, on fixe un entier 
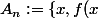non nul et on note \geq M-\frac 1n \})
. On a que }dx\geq \lambda(A_n)\exp\(t\(M-\frac 1n\)\))
donc }dx\)\geq \frac{\lambda(A_n)}t+M-\frac 1n)
. On prend la limite inférieure quand tend vers l'infini pour voir que celle-ci est plus grande que 
pour tout .
par lisonn » 29 Oct 2011, 18:37
Waouh merci, je n'aurais pas pensé à chercher aussi compliqué. Je regarderai ça à tête reposée. Il y a juste un passage qui me parait bizarre, lorsqu'on divise par t, on a plutôt : }dx \ge \frac{1}{t} (\lambda (A_n)e^{M-\frac{1}{n}}))
non ?
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :