Inéquation compliqué .
48 messages
- Page 1 sur 3 - 1, 2, 3
Inéquation compliqué .
Bonjours
Je réalise mon exercice pour la rentrée et etant pris dedans un inéquation m'implose le cerveau,
:mur: :marteau: :ptdr: :cry:
je n'arrive pas a la résoudre :
2x((-3x-4)/3)>5x
il n'y a pas de parenthèses mais c'est histoire de dire qu'il y a un trait de fraction ...
Si vous ne comprenez pas les parenthèses dites le moi ^^
Facultatif: Merci de détailler et m'expliquer (enfin ça serait sympas(j'aime apprendre :zen: ))
Je réalise mon exercice pour la rentrée et etant pris dedans un inéquation m'implose le cerveau,
:mur: :marteau: :ptdr: :cry:
je n'arrive pas a la résoudre :
2x((-3x-4)/3)>5x
il n'y a pas de parenthèses mais c'est histoire de dire qu'il y a un trait de fraction ...
Si vous ne comprenez pas les parenthèses dites le moi ^^
Facultatif: Merci de détailler et m'expliquer (enfin ça serait sympas(j'aime apprendre :zen: ))
Voila ça sera plus simple
http://hapshack.com/?v=imag0284.jpg
désolé je ne connais que cette herbergeur
http://hapshack.com/?v=imag0284.jpg
désolé je ne connais que cette herbergeur
Bonjour,
l'inéquation à résoudre est .
.
Ainsi on développe le membre de gauche ce qui donne
La fraction nous dérange, on multiplie donc par le dénominateur qui est ici positif, donc on conserve le sens de l'inégalité, et on obtiens :
- .
.
On fait passer le membre de droite à gauche en retranchant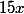 , ainsi on obtient :
, ainsi on obtient :
- , donc -
, donc - .
.
Ainsi on a une inéquation du second degré de la forme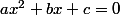 , il faut donc étudier le signe de
, il faut donc étudier le signe de 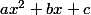 .
.
On commence donc par calculer le discriminant du polynôme
du polynôme 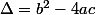 , si
, si 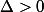 les racines du polynôme sont
les racines du polynôme sont 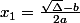 et
et 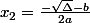 . Si
. Si 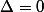 , il y a une unique solution qui est
, il y a une unique solution qui est  . Enfin si
. Enfin si 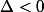 alors l'équation n'a pas de solutions sur
alors l'équation n'a pas de solutions sur  .
.
Ainsi dans notre problème :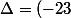^2-4\times(-6)\times(0)=529)
Ainsi et
et  .
.
Tu remplis donc un tableau de signe en gardant en tête qu'un polynôme est du signe de a à l'extérieur des racines.
On obtient alors que - est positif sur
est positif sur 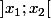 .
.
Cet ensemble est donc solution de l'inéquation de départ.
l'inéquation à résoudre est
Ainsi on développe le membre de gauche ce qui donne
La fraction nous dérange, on multiplie donc par le dénominateur qui est ici positif, donc on conserve le sens de l'inégalité, et on obtiens :
-
On fait passer le membre de droite à gauche en retranchant
-
Ainsi on a une inéquation du second degré de la forme
On commence donc par calculer le discriminant
Ainsi dans notre problème :
Ainsi
Tu remplis donc un tableau de signe en gardant en tête qu'un polynôme est du signe de a à l'extérieur des racines.
On obtient alors que -
Cet ensemble est donc solution de l'inéquation de départ.
Maxwell- a écrit:L'utilité pour lui de donner le résultat comme ça?
Qui plus est ne correspond pas à l'énoncé.
L'utilité là voici, dans son message initial il a écrit
MathOstère a écrit:Merci de détailler et m'explique
Il demande donc une solution détaillée.
Désolé pour l'erreur dans l'énoncé, mais c'est mieux ainsi, car il n'a pas la solution directe, et son inéquation et beaucoup plus simple que celle que j'ai résolu.
Wooh personne ne dors !
Merci pour toute ces réponses l'ennoncé et :résoudre dans IR
puis linéquation excusé moi mon ordinateur avait crashé !
puis linéquation excusé moi mon ordinateur avait crashé !
Maxwell- a écrit:S'il t'avait demandé de faire un DM de 728 pages et de le détaillé tu l'aurais fais ?
Bien évidemment que non je me serai contenté de donner des pistes théoriques mais précises, j'ai réalisé sa demande parce que cela ne demande pas énormément de travail. Si maintenant nous devons justifier nos actes on est pas rendu, pour moi le débat dans lequel nous nous lançons et inintéressant et surtout stérile.
48 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
