Problème limites
14 messages
- Page 1 sur 1
Problème limites
Bonjour , j'ai quelque problèmes pour un exercice
Soit f la fonction définie sur ]-inf ; -2[ par f(x)=(3x²-8x+5)/(x-2)
C est sa courbe représentative dans un repère (O:i,j) et "Delta" et la droite d'équation y=3x-2
la première question était : déterminer la limite de f en 2 . interpréter graphiquement ce résultat , donc pour cette question je pense avoir bon j'ai trouvé que la limite était de +inf , et j'ai donc tracé une asymptote verticale en x=2 , par contre elle croise f(x) et y=3x-2 ( j'ai tracé ces deux courbes aussi ^^) Alors je suis pas sure que ce soit bon
la deuxième question :déterminer la lilmite de f en -Inf donc ca donne f(x) = +inf/-inf , donc du coup c'est une forme indéterminé et donc aprés je ne sais pas comment faire
et la troisième question que je ne comprend pas : Monter que la droite "Delta" est une asymptote à la courbe C . étiduer la position de C par rapport à "Delta"
Voila merci de bien vouloir m'aider :)
Soit f la fonction définie sur ]-inf ; -2[ par f(x)=(3x²-8x+5)/(x-2)
C est sa courbe représentative dans un repère (O:i,j) et "Delta" et la droite d'équation y=3x-2
la première question était : déterminer la limite de f en 2 . interpréter graphiquement ce résultat , donc pour cette question je pense avoir bon j'ai trouvé que la limite était de +inf , et j'ai donc tracé une asymptote verticale en x=2 , par contre elle croise f(x) et y=3x-2 ( j'ai tracé ces deux courbes aussi ^^) Alors je suis pas sure que ce soit bon
la deuxième question :déterminer la lilmite de f en -Inf donc ca donne f(x) = +inf/-inf , donc du coup c'est une forme indéterminé et donc aprés je ne sais pas comment faire
et la troisième question que je ne comprend pas : Monter que la droite "Delta" est une asymptote à la courbe C . étiduer la position de C par rapport à "Delta"
Voila merci de bien vouloir m'aider :)
Bonjour zizou-10
Le 1ier réflexe est de tracer la courbe de la fonction ( c'est à dire
( c'est à dire ) sur ta calculatrice graphique pour voir "la tête" de cette courbe
) sur ta calculatrice graphique pour voir "la tête" de cette courbe
Voici ce que cela donne :
http://www.wolframalpha.com/input/?i=f%28x%29%3D%283x%C2%B2-8x%2B5%29%2F%28x-2%29
Le 2ième réflexe est de calculer les limites vers un nombre qui est "interdit" (ici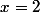 )
)
Dans cet exercice, il faut calculer
=....) (limite à gauche)
(limite à gauche)
et
=...) (limite à droite)
(limite à droite)
pour en déduire que la droite d'équation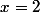 est une asymptote VERTICALE à la courbe
est une asymptote VERTICALE à la courbe 
Le 3ième réflexe est de calculer les limites en et en
et en  (si nécessaire)
(si nécessaire)
Comme
et comme
il est possible que la courbe admette une droite asymptote (dans cet exercice cette asymptote est OBLIQUE) au voisinage de et/ou au voisinage de
et/ou au voisinage de 
Relis ton cours sur les asymptotes, et relis plus attentivement la paragraphe "asymptote oblique à une courbe"
Dans cet exercice, il est précisé que la droite d'équation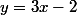 est une asymptote à cette courbe donc il suffit (d'après le cours) de démontrer que ..... ( des explications sont données dans le message ci dessus de gigamesh)
est une asymptote à cette courbe donc il suffit (d'après le cours) de démontrer que ..... ( des explications sont données dans le message ci dessus de gigamesh)
Le 1ier réflexe est de tracer la courbe de la fonction
Voici ce que cela donne :
http://www.wolframalpha.com/input/?i=f%28x%29%3D%283x%C2%B2-8x%2B5%29%2F%28x-2%29
Le 2ième réflexe est de calculer les limites vers un nombre qui est "interdit" (ici
Dans cet exercice, il faut calculer
et
pour en déduire que la droite d'équation
Le 3ième réflexe est de calculer les limites en
Comme
et comme
il est possible que la courbe admette une droite asymptote (dans cet exercice cette asymptote est OBLIQUE) au voisinage de
Relis ton cours sur les asymptotes, et relis plus attentivement la paragraphe "asymptote oblique à une courbe"
Dans cet exercice, il est précisé que la droite d'équation
zizou-10 a écrit:lim 3x²-8x+5=1
x->2+
lim x-2=0+
x->2+
Donc lim f(x)=+inf
x->2+
et
lim 3x²-8x+5=1
x->2-
lim x-2=0-
x->2-
donc lim f(x) = -inf
x->2-
et cela correspond à une asymptote verticale en x= 2
c'est ca?
Oui.
Cependant il n'est pas utile d'étudier la limite lorsque x tend vers 2 à droite,
dans la mesure où ta fonction est définie pour x<2 comme le précise l'énoncé.
Ton prof aura voulu t'éviter de faire deux fois le même type de raisonnement.
De même la limite en +infini n'est pas demandée, dans puisque la contrainte x<2
empêche x de tendre vers +infini...
gigamesh a écrit:Oui.
Cependant il n'est pas utile d'étudier la limite lorsque x tend vers 2 à droite,
dans la mesure où ta fonction est définie pour x<2 comme le précise l'énoncé.
Ton prof aura voulu t'éviter de faire deux fois le même type de raisonnement.
De même la limite en +infini n'est pas demandée, dans puisque la contrainte x<2
empêche x de tendre vers +infini...
c'est pas écrit dans l'énoncé que la fonction est définie pour x<2 ?
Bonsoirzizou-10 a écrit:c'est pas écrit dans l'énoncé que la fonction est définie pour x<2 ?
Désolé , je n'avais pas compris que ton exercice spécifie que :
(à mon avis tu as fait une erreur de frappe dans ton énoncé dans ton 1ier message) donc il faut calculer uniquement les limites aux bornes de cet intervalle c'est à dire :Soit f la fonction définie sur ]-inf ; 2[
quand
et
quand
et en déduire (après avoir fait les calculs adéquates) qu'il y a
une asymptote verticale d'équation
et
une asymptote oblique d'équation
OUI car sur cet intervalle tu ne peux par étudier la limite quandzizou-10 a écrit:Non dans l'énoncer c'est bien ]-inf ; -2 [
Le prof a du se tromper non ?
En -2 la fonction est définie donc quel est l'intérêt d'étudier cette fonction sur ]-inf ; -2 [ ??
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
