Convergence de suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 12:50
par LeJeu » 23 Oct 2011, 12:50
Allez on enchaine...
pour le C : je diviserais haut et bas par le terme le plus grand soit 3^n
pour le D on doit pouvoir tenter la même chose
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 12:58
par Dante0 » 23 Oct 2011, 12:58
LeJeu a écrit:Allez on enchaine...
pour le C : je diviserais haut et bas par le terme le plus grand soit 3^n
pour le D on doit pouvoir tenter la même chose
Ce que j'ai fait est juste pour la 1ere donc ? J'ai pas compris la réflexion de Bony ...
Sinon :
^n-1}{1+(\frac{2}{3^})^n})
Comme
^n = 0)
Alors
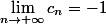
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 23 Oct 2011, 13:04
par Bony » 23 Oct 2011, 13:04
En fait tu peux pas parler de la parité de n lorsque tu fais tendre n vers l'infini, mais l'idée est là.
Est-ce que tu sais que si tu prends 2 suites extraites qui convergent vers la même limite, alors la suite converge vers cette limite?
Par exemple, u(n) = (-1)^n + n
u(2n) = 2n + 1
u(2n+1) = 2n les deux tendent vers l'infini donc u(n) tend vers l'infini
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 13:08
par LeJeu » 23 Oct 2011, 13:08
on converge....
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 13:13
par Dante0 » 23 Oct 2011, 13:13
Bony a écrit:En fait tu peux pas parler de la parité de n lorsque tu fais tendre n vers l'infini, mais l'idée est là.
Est-ce que tu sais que si tu prends 2 suites extraites qui convergent vers la même limite, alors la suite converge vers cette limite?
Par exemple, u(n) = (-1)^n + n
u(2n) = 2n + 1
u(2n+1) = 2n les deux tendent vers l'infini donc u(n) tend vers l'infini
Pourquoi ?
Non je saisis pas ton exemple avec les suites extraites ...
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 23 Oct 2011, 13:15
par Bony » 23 Oct 2011, 13:15
Lorsque tu fais tendre n vers l'infini, tu ne lui attribues pas une valeur fiXe puisque par définition tu le fais varier. Tu ne peuX donc pas arbitrairement dire qu'il est pair / impair
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 13:19
par LeJeu » 23 Oct 2011, 13:19
Je pense que vous êtes d'accord tous les deux !
Dantes étudiait 2 cas : n pair / n impair
Bony : propose deux suites extraites
C'est un peu pareil ?
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 23 Oct 2011, 13:41
par SaintAmand » 23 Oct 2011, 13:41
Dante0 a écrit:...
Bon qu'est-ce qui est faux dans ce que j'ai mis ? Parce que si tout le monde propose une méthode différente on est pas sorti de l'auberge.
Il y a souvent plusieurs méthodes.
Et une bête majoration

?
Quel esr le problème avec ma méthode ? Même au lycée on faisait ca.
Je n'ai pas commenté ta méthode.
En quelle classe es-tu ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 15:10
par Dante0 » 23 Oct 2011, 15:10
SaintAmand a écrit:Il y a souvent plusieurs méthodes.
Et une bête majoration

?
Je n'ai pas commenté ta méthode.
En quelle classe es-tu ?
Bon bah si ma méthode fonctionne , on va pas en faire toute une histoire. :lol3:
Je suis en bac +1. Je ne fais pas des études de maths.
Ok donc on passe à la suivant , vous avez jeté un oeil à mon message de 13h58 ?
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 23 Oct 2011, 15:20
par Bony » 23 Oct 2011, 15:20
c'est juste
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 17:00
par Dante0 » 23 Oct 2011, 17:00
D'accord.
J'imagine que c'est la même méthode pour la suivante.
Quid de la dernière je factorise par n ?
^n)}{n(1+\frac{1}{n}))
du coup je me retrouve encore avec une FI.
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 17:04
par LeJeu » 23 Oct 2011, 17:04
J'aurais simplement regroupé n / (n+1) ?
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 23 Oct 2011, 17:44
par Bony » 23 Oct 2011, 17:44
Raisonne avec ta tête.
Quand n devient très grand, tu peux dire grosso modo que n+1 = n d'accord?
Donc ta suite quand n devient très grand c'est comme si c'était 3*n*(1/2)^n / n donc 3*(1/2)^n donc ça tend vers ?
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 23 Oct 2011, 17:56
par LeJeu » 23 Oct 2011, 17:56
Bony a écrit:Raisonne avec ta tête.
Intérêt de cette remarque?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 23 Oct 2011, 17:59
par Dante0 » 23 Oct 2011, 17:59
Bony a écrit:Raisonne avec ta tête.
Quand n devient très grand, tu peux dire grosso modo que n+1 = n d'accord?
Donc ta suite quand n devient très grand c'est comme si c'était 3*n*(1/2)^n / n donc 3*(1/2)^n donc ça tend vers ?
Bah 0 ?
On aurait pu effectivement poser
.3.(\frac{1}{2})^n)
Et comme la limite des 2 est 0 ...
-
Bony
- Membre Relatif
- Messages: 123
- Enregistré le: 11 Oct 2011, 20:54
-
 par Bony » 23 Oct 2011, 18:02
par Bony » 23 Oct 2011, 18:02
Voilà.
@LeJeu arrête de faire ton justicier à 2 francs tu comprends rien à rien
-
ft73
- Membre Relatif
- Messages: 194
- Enregistré le: 01 Déc 2008, 15:49
-
 par ft73 » 23 Oct 2011, 18:32
par ft73 » 23 Oct 2011, 18:32
Dante0 a écrit:Bah 0 ?
On aurait pu effectivement poser
.3.(\frac{1}{2})^n)
Et comme la limite des 2 est
0 ...
Bony a écrit:Voilà.
Ben non, pas voilà, tu comprends rien à rien.
n/(n+1)->1
Raisonne avec ta tête mon gars.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
?
