Les developpements limites

[kokorico06]

bonsoir,
est-ce que quelqu'un pourrait me faire le raisonnement complet pour trouver la limite en 1 de (sqrt(x+3) - raccubique(3x+5) ) / (1 - tan((Pi*x)/4)) ???

Pck je l'ai fait avec la règle de l'hopital mais ce n'est pas le but de l'exo ! On me demande de le faire avec les DL!

Merci bcp d'avance

[Bony]

Par exemple :

sqrt(x+3) = sqrt(4+x-1) = sqrt(4) * sqrt(1+(x-1)/4)

tu connais le dl de sqrt(1+X) en 0

[Skullkid]

Bonjour, avant toute chose, toutes les DL et équivalents classiques sont donnés en 0. Ici, tu étudies une limite en 1, donc la première chose à faire est de faire un changement de variable pour se ramener en 0. Ensuite, tu peux étudier le numérateur et le dénominateur séparément. En effet, on te demande juste la limite, donc il te suffit de trouver un équivalent du numérateur et un équivalent du dénominateur.

Pour trouver l'équivalent du numérateur, tu fais un DL de chacune des racines, à un ordre suffisant (avec de l'entraînement on peut repérer l'ordre dont on a besoin, sinon tu essayes à l'ordre 1, puis si ça marche pas tu passes à l'ordre 2, etc). Pour le dénominateur, une formule de trigo devrait suffire.

[dhauteval]

Pour le numérateur tu poses x=t+1 pour te ramener à un DL au voisinage de 0 et tu développes [(1+u) puissance z] avec resp. u=t/4 et z=1/2 puis u=(3t)/8 et z=1/3. Si mes calculs sont bons le numérateur est équivalent à (t*t)/64.
Idem et moins de calculs pour le dénominateur en utilisant la formule trigo tan(a+b).

[kokorico06]

En fait je ne comprend pas l'intéret des DL ... le truc c'est qu'on a (par exemple) sqrt(x+3) et qu'on veut le changer en une autre fonction qui a la même limite en 1 que sqrt(x+3) ??? Notre prof ne nous a pas fait la leçon qu'il nous donne déjà des exos dessus.

Bon j'ai essayé pour sqrt(x+3)
donc j'ai trouvé sqrt(x+3) = 2*sqrt(1+X) avec X = (x-1)/4

donc j'ai utilisé le DL de sqrt(1+X) à l'ordre 1 ... j'obtiens (1+X)^(1/2) = 1 + (1/2)*X

du coup sqrt(x+3) = 2 + (x-1)/4 .... Bon très bien mais quel est l'intéret ???
Je comprend juste que sqrt(x+1) a la même limite (en 1) que 2 + (x-1)/4 cad 2! MAis bon à part ça je comprend pas pk on utilise les DL! :( c'est tellement plus simple avec l'Hopital

[Bony]

Le principe des developpements limités est d'avoir "facilement" des limites un peu tordues.

Exemple simple : On veut la limite en 0 de f(x) = x*(exp(x)-1)/(cos(x)-1)

DL de exp(x) = 1 + x + o(x)
DL de cos(x) = 1 - x²/2

On remplace -> f(x) = x*(1+x-1)/(1-x²/2-1) + o (1) = -2 + o(1)

Donc la limite est -2

[Skullkid]

L'intérêt du DL ce n'est pas de remplacer une fonction par une autre qui a la même limite, c'est de remplacer une fonction par un polynôme qui a le même comportement (ce qui est plus fort que "avoir la même limite").

L'intérêt d'avoir un polynôme, c'est que tu sais facilement calculer des sommes et produits de polynômes, alors que des sommes de cosinus ou de racines cubiques, c'est nettement plus dur.

L'information contenue dans le DL à l'ordre n de f en a c'est "tel polynôme est le polynôme de degré inférieur ou égal à n qui approche le mieux f autour de a", c'est beaucoup plus puissant que la règle de l'Hôpital.

Par exemple, le polynôme de degré inférieur à 2 qui approche le mieux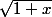 autour de 0 c'est . Mais attention, ça ne veut certainement pas dire que , ça veut dire que est une quantité qui tend vers 0 en 0, "plus vite" que x². Plus précisément, ça signifie exactement que

Après, si tu n'as pas encore eu de cours dessus, je comprends que tu sois un peu perdu... Souviens-toi juste que l'idée derrière un DL c'est de trouver le meilleur polynôme qui approche f.

[kokorico06]

Ok merci bcp à vous, c'est vrai que là j'étais un peu bcp noyée ^^. Mais je vois mieux l'intérêt d'utiliser les DL c'est déjà pas mal :).

Merci bcp encore une fois !

[kokorico06]

Est-ce que ça veut dire que plus l'ordre que l'on choisi est grand et plus la fonction trouvée se rapprochera de la fonction de départ ?

[Skullkid]

Est-ce que ça veut dire que plus l'ordre que l'on choisi est grand et plus la fonction trouvée se rapprochera de la fonction de départ ?

Oui, plus l'ordre est grand, plus tu approches ta fonction avec précision. Intuitivement, si tu prends la courbe d'un polynôme de degré n, elle d'autant moins "rigide" que n est grand. Pour n=1, tu auras toujours une droite, tu ne peux jouer que sur deux paramètres : le coefficient directeur et l'ordonnée à l'origine. Pour n=2 tu auras toujours une parabole, tu peux jouer sur trois paramètres, etc. Plus tu as de paramètres sur lesquels jouer, mieux tu peux approcher. En contrepartie, en général, plus le nombre de paramètres est grand, plus longs sont les calculs. Un des enjeux quand on fait des DL c'est de savoir de quoi on a vraiment besoin : si un polynôme de degré 1 te suffit, ce n'est pas la peine de chercher un polynôme de degré 4.

Par exemple, si je veux un équivalent en 0 de , un DL à l'ordre 1 ne suffit pas, parce que j'obtiens (as-tu vu en cours cette notation o(x) ?). Ce DL à l'ordre 1 me dit juste que f(x) tend vers 0 plus vite que x, ce qui est mieux que rien, mais ça ne me donne pas d'équivalent. Pour avoir l'équivalent, il faut pousser à l'ordre 2, et on obtient , qui est une information plus précise : ça dit que .

[kokorico06]

Pour sqrt(x+3) j'ai trouvé sqrt(1+X) avec X = (x-1)/2

mais dans la formule des DL a l'ordre 2 on dit que c'est 1+X/2 ... ou 1+x/2 ?
Est-ce qu'on garde le x du départ ou est-ce qu'on prend le X du changement de variable ??
Sinon pour la notation o(X²) je connais oui !

[kokorico06]

Autre question: est-ce qu'on doit prendre le même ordre pour chaque "partie" de la fonction ou est-ce que je peux prendre l'ordre 2 pour sqrt(x+3) et puis un autre ordre pour le dénominateur par exemple ?

[Skullkid]

Tu es libre de choisir tes ordres comme tu l'entends. Ce qui est important de savoir comment les "recombiner" après.

Par exemple, si tu fais la somme d'un DL de f à l'ordre 1 et d'un DL de g à l'ordre 4, tu obtiendras un DL de f+g à l'ordre 1 : tous les termes d'ordre supérieur ou égal à 2 du DL de g seront "absorbés" par le o(x) du DL à l'ordre 1 de f. C'est pour ça qu'il est très important de ne jamais oublier les o() : ce sont eux qui te disent à quel ordre tu es.

Donc, ici, si tu veux un DL2 de , il te faut faire un DL2 de 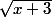et un DL2 de .

Pour ce qui est des x de départ ou non, ce sont toujours les "nouvelles" variables qu'il faut garder. Par exemple, le DL de la racine carrée te dit que au voisinage de 0 : c'est le même x dans le membre de gauche et dans le membre de droite. Si tu veux développer , tu obtiens .

[kokorico06]

Ok merci pour les réponses rapides et simples :)

Bonne soirée !