Relations trigonométriques... :/
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dRoxanne
- Messages: 6
- Enregistré le: 17 Oct 2011, 10:30
-
 par dRoxanne » 17 Oct 2011, 10:36
par dRoxanne » 17 Oct 2011, 10:36
Bonjour, bonjour à tout le monde !
Je suis là car j'ai besoin d'un petit coup de pouce, je ne sais pas vraiment par où commencer ni quoi faire ... Enfin si, j'essaye mais je ne parviens jms au résultat souhaité!
Quoiqu'il en soit je commence, alors l'énoncé est le suivant ,
Démontrer que pour tout x de R, on a la relation:
sin^4(x)= 3/8-1/2 cos 2 (x) + 1/8 cos 4 (x)
.... Voilà, donc j'ai commencer par sin^4(x)=(sin^2(x))^2=((1-cos 2(x))/2)^2 je développe et c'est n'importe quoi lol
help please ^^ Merci =)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 17 Oct 2011, 10:37
par XENSECP » 17 Oct 2011, 10:37
}^4 = \dfrac 38 - \dfrac 12 \cos{(2x)} + \dfrac 18 \cos{(4x)})
c'est ça ?
-
dRoxanne
- Messages: 6
- Enregistré le: 17 Oct 2011, 10:30
-
 par dRoxanne » 17 Oct 2011, 10:44
par dRoxanne » 17 Oct 2011, 10:44
ouaip c'est bien ça ^^ =)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 17 Oct 2011, 10:48
par XENSECP » 17 Oct 2011, 10:48
Ca te dirait pas de le faire à l'envers ??
Genre cos(4x) = 1 - 2 sin(2x)^2
avec sin(2x) = 2sin(x)cos(x)
...
Tu essayes de tout passer en sin(x) et tu regroupes ;)
-
dRoxanne
- Messages: 6
- Enregistré le: 17 Oct 2011, 10:30
-
 par dRoxanne » 17 Oct 2011, 10:49
par dRoxanne » 17 Oct 2011, 10:49
arf ... je comprends vraiment pas grand chose à ce truc, je crois que j'ai pas très bien saisi les relations trigonométriques dans ce cas de figure, y'aurait-il moyen d'avoir davantage de précisions et d'explications? :'(
-
Anonyme
 par Anonyme » 17 Oct 2011, 10:56
par Anonyme » 17 Oct 2011, 10:56
dRoxanne a écrit:sin^4(x)= 3/8-1/2 cos (2x) + 1/8 cos (4x)
Bonjour
Attention de placer correctement les parenthèses dans ton énoncé (
voir corrections en rouge).
Il y a différentes méthodes pour démontrer cette égalité.
Si tu es en classe de terminale S et que tu as étudié les nombres complexes alors tu peux utiliser l'exponentielle complexe
Ce qui revient à écrire que :
cos(2x) = [e^(2 i x) + e^(-2 i x)] / 2
cos(4x) = [e^(4 i x) + e^(-4 i x)] / 2
[sin(x)]^4= ( [e^(i x) - e^(-i x)] / 2i )^4
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 17 Oct 2011, 11:29
par XENSECP » 17 Oct 2011, 11:29
schulhof_2 a écrit:sin^4(x)= ( [e^(4 i x) - e^(-4 i x)] / 2i )^4
Euh sans 4 dans les parenthèses des exp

-
Anonyme
 par Anonyme » 17 Oct 2011, 11:42
par Anonyme » 17 Oct 2011, 11:42
XENSECP a écrit:Euh sans 4 dans les parenthèses des exp

Merci , petite erreur corrigée... sin(x)^4=.........
Commentaire:
Il ne faut pas confondre les différentes notations avec des parenthèses.
sin^4(x)=sin(x)^4
et
sin(4x)
 par busard_des_roseaux » 17 Oct 2011, 11:42
par busard_des_roseaux » 17 Oct 2011, 11:42
1er méthode: Formule de
De Moivre= (\frac{e^{ix}-e^{-ix}}{2i})^4)
et tu développe avec la formule du binome dont voici les coefficients: 1 4 6 4 1
2ème méthode: à la main
=(\frac{1-cos \, 2x}{2})^2=\frac{1}{4} \left( 1-2 cos \, 2x + \frac{1+cos \, 4x}{2} \right))
-
Anonyme
 par Anonyme » 17 Oct 2011, 14:08
par Anonyme » 17 Oct 2011, 14:08
busard_des_roseaux a écrit:1er méthode: Formule de
De Moivre= (\frac{e^{ix}-e^{-ix}}{2i})^4)
et tu développe avec la formule du binome dont voici les coefficients: 1 4 6 4 1
Ce qu'on appelle la "formule de Moivre"
n'est ni plus ni moins :
une règle sur les puissances que l'on applique à l'exponentielle complexe, c'est à dire à
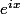
:
^4= e^{i4x})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
