Prolongement analytique

[pacman314]

Bonsoir ;

Voila j'ai un éxercice ou je considère une série entiere ou z est complexe et on me demande de montrer qu'il est impossible de trouver U ouvert connexe et une fonction holomorphe g sur U tel que U ne soit pas entièrement contenu dans D(0,1)

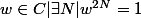
Quand je regarde la correction on me dit que cela découle du fait que l'ensemble est dense dans le cercle unité et du théoreme de prolongement analytique .

En fait je ne comprends pas a quoi sert la 1ere donnée . Mon raisonnement est le suivant . Supposons qu'il existe cette fonction g . Alors comme est un ouvert comme intersection de 2 ouverts . on applique le principe de prolongement analytique et donc f=g sur tout l'ouvert connexe . D'ou la contradiction , et donc que .

Merci de l'aide .

[Doraki]

Où est-ce que t'u t'es servi de l'hypothèse U non inclus dans D pour obtenir ta contradiction ?

Aussi, fais gaffe, l'intersection de deux ouverts connexes n'est pas forcément connexe donc tu peux avoir du mal à appliquer ton théorème sur l'intersection de U et de D.


Et puis il me semble bien que g(z) = 1/(1-z²) prolonge f sur C\{1,-1}, qui contient strictement D.

[pacman314]

Bonjour Doraki .

Il me semble que pour appliquer le principe du prolongement analytique il suffit que f=g sur un ouvert contenu dans un ouvert connexe pour que f=g sur cet ouvert connexe ,ce qui implique que f=g sur U. Or comme f=g sur D(0,1) ;

J'en deduis donc que ta fonction que tu donnes g est developable en serie de taylor au point 0 sur l'ouvert (on suppose que U non inclu dans D(0,1)) et de somme la serie f que j'ai défini . Or on sait justement que t'as fonction g est developpable en 0 en série de taylor uniquement sur D(0,1) ,ailleur la série diverge de toute facon . D'ou la contradiction sur le fait que U ne soit pas inclu dans D(0,1).

Dis moi ou je foire parce que la je dois avoir un gros probleme de compréhension .

Merci a+

[Doraki]

L'énoncé de la question, c'est bien "montrer qu'il n'existe pas d'ouvert U et de fonction g holomorphe sur U tels que U inter D est non vide, U n'est pas inclus dans D, U est connexe, et pour tout z de U inter D, f(z) = g(z)" ?

[pacman314]

oui c'cela ,on suppose que U non entierement contenue dasn D(0,1) aussi

[Doraki]

Il me semble que pour appliquer le principe du prolongement analytique il suffit que f=g sur un ouvert contenu dans un ouvert connexe pour que f=g sur cet ouvert connexe ,ce qui implique que f=g sur U.

Oui mais nous on a f définie sur D et g définie sur U donc tu peux pas parler de f=g sur ailleurs que U inter D, et ça c'est déjà dans les hypothèses de la question alors j'vois pas ce que tu veux faire de plus.


Tu peux vérifier que pour tout z dans U = C\{-1,1}, ma fonction g(z)=1/(1-z²) est développable en série entière au point z, et le rayon de convergence de cette série se trouve être la distance de z à {-1,1}
(et que la question ne peut pas être correcte vu que c'est un contre-exemple)

[pacman314]

pourquoi ? on ne peut pas dire que f=g sur U et f=g sur D alors f=g sur U et D.

[Doraki]

f n'existe pas sur la partie de U qui dépasse de D alors arrête de dire que f=g dessus.
(et de même pour g si U ne contient pas D en entier)

[pacman314]

ben justement c'est la la contradiction . on met en defaut le principe du prolongement analytique ce qui est contradictoire .

[Doraki]

J'vois pas comment tu peux appliquer ce principe sur autre chose que U inter D (qui peut même ne pas être connexe), où on sait déjà que f=g parceque c'est dans l'énoncé de la question que j'ai remise. Donc ce principe ne sert à rien du tout ici.

[pacman314]

Si il sert puisque la correction s'en sert ,non pas que je ne veuille pas te croire . De plus j'ai essayé de donner une explication plus haut post 3 . Je sais bien que f non definie ailleur que sur D(0,1) d'ou la contradiction avec le prologement anlytique qui dit que f=g sur U ouvert connexe ssi il existe un ouvert G inclu dans U tel que f=g sur G

[Doraki]

dans les hypothèses du théorème du prolongement analytique, il y a bien sûr que f et g doivent exister sur l'ouvert U connexe dans lequel tu trouves G.

sinon j'vois pas ce qui t'empêche de dire :

"Soit f(z) = 0 sur D(0,2) et soit g(z) = 0 sur D(1,2).
f = g sur D(0,2) inter D(1,2), donc f = g sur D(0,2).
Donc g(-1) = 0. Ah ben mince alors g(-1) ça n'existe pas, contradiction !!!"

[pacman314]

oui mais g est defini sur U et nous justement on veut montrer qu il est impossible de definir une fonction holomorphe sur U tel que que U ne soit pas contenue entierement dans D . D'ou avec ce que tu viens d'ajouter peut etre l'utilité de la densité que je ne comprends pas va faire son apparition ..... Mais bon la j'avoue que je coince alors.

[Doraki]

Mais tu veux montrer un truc faux vu que U et g tels que blablabla existent.

[pacman314]

Comment sa je veux montrer un truc faux ? je pense qu'il veule me faire dire le rayon de convergence de f en tout point z0 inclu dans D(0,1) qui serait alors |1-z0|

[Doraki]

Bah si la question c'est

"montrer qu'il n'existe pas d'ouvert U de C et de fonction g holomorphe sur U tels que U inter D est non vide, U n'est pas inclus dans D, U est connexe, et pour tout z de U inter D, f(z) = g(z)" ?

c'est impossible.

Ptetre que t'as mal lu.

[pacman314]

oui c'est sa y faut montrer que c'est impossible lol . Sinon je viens de relire l'énoncé y a pas de doute c'est sa qui est demandé.

[Doraki]

je disais que c'est impossible de montrer que c'est impossible qu'il y ait U et g tels que blablabla

[pacman314]

donc la réponse qu ils m ont donné est incorrect ? je trouve sa assez douteux quand meme .... Va me dire ce que t'en pense http://exo7.emath.fr/ficpdf/fic00075.pdf . C est l'exo 17