Fonction, tangente a une courbe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 13:55
par Grugh » 23 Jan 2011, 13:55
Bonsoir, voila j'ai un petit soucis pour finir mon exercice, pourriez vous m'aider svp? Merci d'avance, voici l'énoncé:
Soit g la fonction définie sur g(x)=x² et de courbe (C).
1°) Donner l'équation de la tangente (Ta) à (C) au point (a;g(a))
2°)démontrer que (P) est entièrement au dessus de toutes ses tangentes.
3°)Démontrer que (Ta) coupe l'axe des ordonnées en un point K d'ordonnée négative.
4)) Calculer l'aire du triangle OAK en fonction de a.
Mes résultats :
1°) Je trouve comme équation : 2ax +a².
2°)On cherche donc à résoudre x²-2ax+a²0.
Or x²-2ax+a²=(x-a)² , donc tjrs positif.
3°)Ta : y=2ax-a²
Elle coupe (Oy) au pointd'abscisse 0 : x=0 ---> y=-a² qui est bien une ordonnée négative.
4°)C'est pour cette question que je bloque. Merci d'avance pour votre aide.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 14:36
par Sa Majesté » 23 Jan 2011, 14:36
Salut
Tu peux par exemple trouver l'équation de la droite (KA) puis trouver les coordonnées du projeté orthogonal H de O sur (KA)
La droite (OH) est une hauteur du triangle OAK
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 14:38
par XENSECP » 23 Jan 2011, 14:38
Sa Majesté a écrit:Salut
Tu peux par exemple trouver l'équation de la droite (KA) puis trouver les coordonnées du projeté orthogonal H de O sur (KA)
La droite (OH) est une hauteur du triangle OAK
Ou bien appliquer la formule du cours que j'écris 4 fois par jour en ce moment :
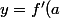 (x-a) + f(a))
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 14:42
par Grugh » 23 Jan 2011, 14:42
Je dios avouer que je suis un peu perdu, cette formule peut s'appliquer pour (KA)?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 14:49
par Sa Majesté » 23 Jan 2011, 14:49
XENSECP a écrit:Ou bien appliquer la formule du cours que j'écris 4 fois par jour en ce moment :
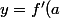 (x-a) + f(a))
Euh ... je répondais à la question 4, la seule qui pose problème
Là tu mets l'équation de la tangente :lol3:
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 14:57
par Grugh » 23 Jan 2011, 14:57
Ah donc je n'ai pas besoin de cette formule pour la 4°)?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 14:59
par Sa Majesté » 23 Jan 2011, 14:59
Ben en fait la droite (AK) c'est la tangente en A à (C) ...
Donc l'équation tu l'as déjà (attention c'est y=2ax-a², faute de frappe dans ce que tu as écrit)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 14:59
par XENSECP » 23 Jan 2011, 14:59
Sa Majesté a écrit:Euh ... je répondais à la question 4, la seule qui pose problème
Là tu mets l'équation de la tangente :lol3:
Autant pour moi, je n'avais pas vu les réponses déjà faites ... :dodo:
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 15:07
par Grugh » 23 Jan 2011, 15:07
Sa Majesté a écrit:Ben en fait la droite (AK) c'est la tangente en A à (C) ...
Donc l'équation tu l'as déjà (attention c'est y=2ax-a², faute de frappe dans ce que tu as écrit)
Ah oui, c'est vrai . Par contre je suis toujours aussi perdu :mur:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 15:10
par Sa Majesté » 23 Jan 2011, 15:10
Il faut trouver les coordonnées du projeté orthogonal H de O sur (KA)
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 15:13
par Grugh » 23 Jan 2011, 15:13
Sa Majesté a écrit:Il faut trouver les coordonnées du projeté orthogonal H de O sur (KA)
Le projeté orthogonal?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 15:15
par Sa Majesté » 23 Jan 2011, 15:15
Oui
Comme ça tu auras une hauteur du triangle OAK donc tu pourras trouver son aire
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 15:17
par Grugh » 23 Jan 2011, 15:17
Ok je rois comprend mais je ne sais pas ce qu'est un projeté orthogonal, c'est ce qui mle pose problème. Merci

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 15:23
par Sa Majesté » 23 Jan 2011, 15:23
Tu es au moins en 1ère non ?
Ce n'est pas possible que tu n'aies jamais entendu parler de projection orthogonale
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 15:24
par Grugh » 23 Jan 2011, 15:24
Oui je suis en 1ère et j'en ai entendue parler qu'une fois mais assez rapidement, donc je ne m'en souviens plus du tout.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 15:29
par XENSECP » 23 Jan 2011, 15:29
Si je peux me permettre (pour pas y passer la nuit), on a O et K sur l'axe des ordonnées donc une hauteur du triangle serait juste celle issue de A... et la distance bah c'est x_A = a.
Donc hauteur * base / 2 = OK * a / 2 = -a^2 * a / 2 = -a^3/2
sauf erreur de ma part ;)
-
Grugh
- Membre Naturel
- Messages: 89
- Enregistré le: 06 Oct 2010, 14:37
-
 par Grugh » 23 Jan 2011, 15:33
par Grugh » 23 Jan 2011, 15:33
XENSECP a écrit:Si je peux me permettre (pour pas y passer la nuit), on a O et K sur l'axe des ordonnées donc une hauteur du triangle serait juste celle issue de A... et la distance bah c'est x_A = a.
Donc hauteur * base / 2 = OK * a / 2 = -a^2 * a / 2 = -a^3/2
sauf erreur de ma part

Je comprend ta démarche, et avec la hauteur je pourrais calculer l'aire?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 15:33
par XENSECP » 23 Jan 2011, 15:33
Grugh a écrit:Je comprend ta démarche, et avec la hauteur je pourrais calculer l'aire?
-_-'
Là tu me déprimes j'interviens plus !
(j'ai écris tout le calcul précédemment donc faut suivre)

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 15:34
par Sa Majesté » 23 Jan 2011, 15:34
Grugh a écrit:Je comprend ta démarche, et avec la hauteur je pourrais calculer l'aire?
Si tu écris ça, c'est que tu n'as pas compris la démarche ! :ptdr:

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 23 Jan 2011, 15:34
par Sa Majesté » 23 Jan 2011, 15:34
XENSECP a écrit:Si je peux me permettre (pour pas y passer la nuit), on a O et K sur l'axe des ordonnées donc une hauteur du triangle serait juste celle issue de A... et la distance bah c'est x_A = a.
Donc hauteur * base / 2 = OK * a / 2 = -a^2 * a / 2 = -a^3/2
sauf erreur de ma part

OK mais il manque des valeurs absolues
:lol3:
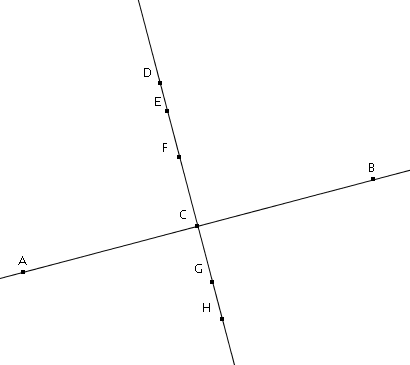
Sinon pour Grugh
Dans la figure ci-dessous, D, E, F, G et H ont pour projeté orthogonal C sur (AB)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités

