Fonctions continues et équations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 10:11
par Anonyme. » 23 Jan 2011, 10:11
Bonjour, voila j'ai un exercice à faire mais je bloque lors d'une étape, a vrai dire la premiere
Voici l'énoncé :
1) Démontrer que l'équation 3x - 10 + (12/x²) = 0 admet exactement deux solutions et que ces deux solutions appartiennent à ]0;+infini[
2) Déterminer une valeur approchée de chacune des deux solutions à 10^-2 près
Pour la premiere j'ai décidé de trouver la dérivée de l'équation pour trouver ensuite les solutions
je trouve une dérivée qui me semble improbable car je ne sais pas comment faire pour trouver les solutions a partir de celle ci
dérivée : 3 + (24x/x^4)
Je voudrais avoir votre avis. Merci d'avance
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 10:46
par XENSECP » 23 Jan 2011, 10:46
Pour la première, il faut faire la dérivée effectivement. Tu peux d'ailleurs simplifier par x.
Ensuite étudie le signe, fait le tableau de variations et tu pourras utiliser le théorème des valeurs intermédiaires.
-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 10:50
par Anonyme. » 23 Jan 2011, 10:50
Donc d'apres toi ma dérivée est correcte ? Car je n'arrive pas a étudier le signe de cette dérivée... en cours nous étudions le signe de fonctions polynome par exemple ( 3x² - 2x + 4) La je ne sais pas comment m'y prendre
Apres ca devrait aller, j'utiliserais le théoreme des valeurs intermédiaires ou le théoreme de la bijection
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 10:52
par XENSECP » 23 Jan 2011, 10:52
Mets au même dénominateur ;)
-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 10:55
par Anonyme. » 23 Jan 2011, 10:55
(3x^3+24)/x^3 si je ne me suis pas trompé
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 10:57
par XENSECP » 23 Jan 2011, 10:57
Anonyme. a écrit:(3x^3+24)/x^3 si je ne me suis pas trompé
Ca m'a l'air bien.
Maintenant bah
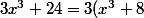)
et tu sais que
^3 = -8)
donc ça te donne déjà une racine évidente pour factoriser et donc connaître le signe.
-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 11:07
par Anonyme. » 23 Jan 2011, 11:07
D'accord donc quand je remplace x par la racine évidente -2, je trouve 3x^3 + 24 = 0
Mais j'ai encore un x^3 au dénominateur ...
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 11:12
par XENSECP » 23 Jan 2011, 11:12
...
Euh -2 comme racine évidente, ça veut juste dire que
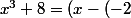)(ax^2+bx+c))
Il faut donc trouver a,b et c. Essayer de refactoriser et dans tous les cas trouver le signe de tout ça.
Pour x^3 tu connais son signe

-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 11:21
par Anonyme. » 23 Jan 2011, 11:21
J'avais effectivement l'idée de faire ça
x^3 + 8 = (x+2)(ax²+bx+c)
= ax^3 + bx² + cx + 2ax² + 2bx + 2c
= ax^3 + x²(b+2a) + x(c+2b) + 2c
Mais après je n'arrive plus a avancer, pour moi a = 1 ...
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 11:25
par XENSECP » 23 Jan 2011, 11:25
b+2a = 0
c+2b = 0
2c = 4
(identification)
-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 11:27
par Anonyme. » 23 Jan 2011, 11:27
Euh je ne comprend pas trop ce raisonnement ...
et pour 2c = 4, ce ne serait pas plutot c = 4 et 2c = 8 ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 11:30
par XENSECP » 23 Jan 2011, 11:30
Pardon ouais c = 4 (j'ai été un peu vite).
Termines le calcul ;)
-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 11:40
par Anonyme. » 23 Jan 2011, 11:40
Donc a = 1 ; b = -2 et c = 4
(x+2)(x²-2x+4)
Maitenant je dois calculer delta = b²-4ac pour le trinome, je trouve les solutions, apres je fais mon tableau de variations puis j'applique le théoreme des valeurs intermediaires ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 11:43
par XENSECP » 23 Jan 2011, 11:43
En quelque sorte.
Tu peux aussi voir que
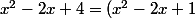+3)
Pour trouver le signe je trouve ça + rapide

-
Anonyme.
- Messages: 8
- Enregistré le: 23 Jan 2011, 10:00
-
 par Anonyme. » 23 Jan 2011, 11:45
par Anonyme. » 23 Jan 2011, 11:45
Ok je vais voir ca, en tous cas je te remercie de ton aide! en esperant que je ne fasse pas d'erreurs pour la suite ... ;)
Merci encore et bonne journée ;)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
