Produit scalaire
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 08:55
par nicolas202 » 23 Jan 2011, 08:55
Bonjour, je dois faire un exercice mais je suis bloqué à la question 3. Pourriez- vous m'aider et me donner des pistes ?
1/ Construire un triangle ABC sachant que : AB=5 , BC=8 , AC=6
2/ Construire le barycentre : G=bar( (A;1) (B;2) (C;3)
Exprimer le vecteur AG en fonction des vecteurs AB et AC : Je trouve (v=vecteur) :
vAG=(1/3)vAB+(1/2)vAC
3/ Calculer le produit scalaire vAB.vAC. Je suis bloQUÉ.
4/ En déduire la distance GA.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 10:50
par XENSECP » 23 Jan 2011, 10:50
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 11:14
par nicolas202 » 23 Jan 2011, 11:14
Merci mais on ne connait pas le cosinus et on n'a pas encore appris le théorème d'Al kashi donc je n'arrive pas à utiliser cette formule
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 11:24
par XENSECP » 23 Jan 2011, 11:24
Hum. Tu traces la hauteur issue de C et tu seras dans un triangle rectangle. Un rapide calcul pour déterminer AH et ce sera bon.
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 11:27
par nicolas202 » 23 Jan 2011, 11:27
oui mais quel est ce rapide calcul ^^?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 11:29
par XENSECP » 23 Jan 2011, 11:29
Bah tu poses x = AH et avec 2 Pythagore ;)
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 12:37
par nicolas202 » 23 Jan 2011, 12:37
même en utilisant pythagore je n'arrive pas à calculer AH car AH^2=AC^2-CH^2 or on ne connait pas CH
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 12:39
par XENSECP » 23 Jan 2011, 12:39
J'ai dit "2" Pythagore... Faut le faire dans les 2 triangles :
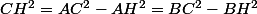
avec
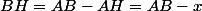
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 12:57
par nicolas202 » 23 Jan 2011, 12:57
je suis d'accord mais c'est BH=AB+x (et non -x)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 12:59
par XENSECP » 23 Jan 2011, 12:59
nicolas202 a écrit:je suis d'accord mais c'est BH=AB+x (et non -x)
Lol, ton point H n'est pas sur [AB] ?
Sinon bah après tu détermines x et tu arriveras à calculer la formule donnée au début
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 13:03
par nicolas202 » 23 Jan 2011, 13:03
non H n'est pas sur AB
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 13:09
par XENSECP » 23 Jan 2011, 13:09
Autant pour moi. Je n'avais fait qu'un dessin à la main.
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 13:14
par nicolas202 » 23 Jan 2011, 13:14
Merci beaucoup :-) mais ensuite je dois trouver la norme de AG et je sais que vectAG=(1/3)vAB+(1/2)vAC . Or je sais que vAB.vAC=-3/2 (ce que je viens de trouver ) mais je ne trouve pas de relation qui lie les deux
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 13:19
par XENSECP » 23 Jan 2011, 13:19
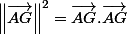
Tu vois mieux ?
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 23 Jan 2011, 13:46
par nicolas202 » 23 Jan 2011, 13:46
comment fais-tu les vecteurs comme ça ? (en les tapant)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 23 Jan 2011, 14:22
par XENSECP » 23 Jan 2011, 14:22
nicolas202 a écrit:comment fais-tu les vecteurs comme ça ? (en les tapant)
Tu fais "citer" et tu vois le code LaTeX utilisé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
