Vecteur et emsemble de points

par **fordson65** » 22 Jan 2011, 09:02

bonjour à tous,

je n'arrive pas à simplifier une écriture vectorielle pour déterminer un ensemble de points:

voila l'affaire : le points O est barycentre du système de points pondérés {(A;1)(B;-1)(C;1)}

je voudrais simplifier cette ecriture vectorielle sachant que

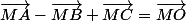
(facile c'est obtenu par definition mais c'est selon moi indispensable pour la suite)

j'aimerais simplifier l'ecriture de gauche :

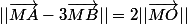
je n'y arrive pas.
merci d'avance

par **Anonyme** » 22 Jan 2011, 09:20

Considère le barycentre de (A,1) et (B,-3) ..

par **fordson65** » 22 Jan 2011, 09:31

je l'ai envisager mais peut on se servir du théorème du barycentre partiel après? si oui je ne voit pas

par **Anonyme** » 22 Jan 2011, 09:34

fordson65 a écrit:je l'ai envisager mais peut on se servir du théorème du barycentre partiel après? si oui je ne voit pas

qu'appelles-tu théorème du barycentre partiel ? Lassociativité ?

par **fordson65** » 22 Jan 2011, 09:39

oui c'est ca excuse moi

par **Anonyme** » 22 Jan 2011, 09:43

Pourquoi veut tu l'utiliser alors que le résultat découle directement ?
Soit J le barycentre de {A,1} , {B,-3} , on a que

Donc on se ramène a

donc ...

par **fordson65** » 22 Jan 2011, 09:49

oui c'est vrai je me suis embêter pour rien :mur: merci beaucoup et bonne journée! :lol3:

par **Anonyme** » 22 Jan 2011, 09:55

Pas de quoi et bonne journée aussi :lol3:

Vecteur et emsemble de points

vecteur et emsemble de points

Qui est en ligne