Bonsoir,
J'aimerais transformer la formule ci-dessous en un polynome qui prenne la forme suivante :
y = ax + by + c
Voici la formule en questions :
i(t) = 1000 * ((Sigma(Qt * Ct) / Bo * Kt )
Est-ce possible .?
Transformation d'une formule en un polynome
3 messages
- Page 1 sur 1
salut,
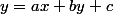 , ca equivaut à
, ca equivaut à
=ax+c) et donc
et donc
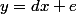 avec d = a/(1-b) et e = c/(1-b)
avec d = a/(1-b) et e = c/(1-b)
ensuite
i(t) = 1000 * ((Sigma(Qt * Ct) / Bo * Kt )
donc = k_1 \bigsum k_2 t)
avec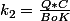 et
et 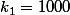
soit encore
 = nk_1k_2t)
avec n le nombre de termes dans la somme.
et on identifie donc
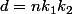 et
et 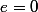
donc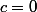 et
et
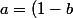d)
donc les solutions pour (a,b,c) sont de la forme
(-d,2,0) ou (d,0,0)
si b=1, alors ax+c=0 et donc x est une constante ce qui ne satisfait pas i(t)
ensuite
i(t) = 1000 * ((Sigma(Qt * Ct) / Bo * Kt )
donc
avec
soit encore
avec n le nombre de termes dans la somme.
et on identifie donc
donc
donc les solutions pour (a,b,c) sont de la forme
(-d,2,0) ou (d,0,0)
si b=1, alors ax+c=0 et donc x est une constante ce qui ne satisfait pas i(t)
la vie est une fête 
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
