Solution de f (rédaction)

par **Youyou30** » 16 Jan 2011, 22:19

salut,

voilà j'ai un exercice je sais qu'il est simple mais le problème réside dans la rédaction !
je ne sais pas comment rédiger
pouvez-vous me venir en aide ?

voici mon exercice:
1/ Soit f une application continue de [o,1] dans [0,1].
Montrer que l'équation f(x)=x a au moins une solution
Merciiiii

par **girdav** » 16 Jan 2011, 22:26

Bonjour,
pose

. Que dire de

?

? De la régularité de

?

par **Youyou30** » 16 Jan 2011, 22:27

elle est strictement croissante ...

par **girdav** » 16 Jan 2011, 22:31

Pas forcément : avec

qui satisfait aux hypothèses on a que

qui est strictement décroissante.

par **Youyou30** » 16 Jan 2011, 22:32

elle est comment alors si elle est souvent décroissante ?
positive ?

par **girdav** » 16 Jan 2011, 22:35

Pour un

dans l'intervalle

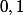
, dire que

revient à dire que

.
Tu n'as toujours pas calculé

.

par **Youyou30** » 16 Jan 2011, 22:38

sii sii g(0)=0 ..

par **girdav** » 16 Jan 2011, 22:42

Pas nécessairement, par exemple toujours dans le cas où

. On sait juste que pour tout

,

.

par **Youyou30** » 16 Jan 2011, 22:44

Okay !
mais comment calculer g(0) si on ne connais pas la fonction f(x) ??

par **girdav** » 16 Jan 2011, 22:46

On a que

. On cherche à appliquer un théorème bien connu sur les fonctions continues.

par **Youyou30** » 16 Jan 2011, 22:50

Oula je sais vraiment pas ...
peut-être le théorème de la bijection ?

par **girdav** » 16 Jan 2011, 22:52

Ou celui des valeurs intermédiaires?

Solution de f (rédaction)

Solution de f (rédaction)

Qui est en ligne