Bonjour. J'ai un devoir à faire et je n'arrive pas du tout à faire le deuxième partie qui porte grosso modo sur les spectres ordonnés. En effet, d'habitude quand on doit montrer quelque chose avec des valeurs propres, il suffit de faire quelque chose du genre "soit

valeur propre,

vecteur propre associé" etc. mais là j'ai l'impression que je suis obligée de travailler avec toutes les valeurs propres à la fois et je ne vois vraiment pas comment faire !
Je ne demande pas forcément les réponses, mais au moins une piste.
Je vous mets les questions de la deuxième partie (dites moi si vous voulez aussi la première) :
Pour
)
(

est un

-espace vectoriel de dimension finie

associé au produit scalaire
)
,
)
est l'ensemble des endomorphismes symétriques), le spectre ordonné de

noté
)
, est l'ensemble de ses valeurs propres (avec leur ordre de multiplicité) ordonnées par ordre décroissant. Si
)
, et si
=\{a_1 \geq a_2 \geq \ldots \geq a_n\})
,
=\{b_1 \geq b_2 \geq \ldots \geq b_n\})
on note
\geq Sp(v))
si, et seulement si

pour
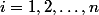
.
1) Soient
)
,

des vecteurs propres de

, deux à deux orthogonaux, et associés à des valeurs propres

. On pose
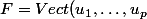)
et
=\{ \frac{(x,u(x)}{(x,x)}; x \in E \})
Déterminer
))
et
))
.
2) Soient
)
.
a) Prouver que si

, alors
 \geq Sp(v))
b) Donner un contre-exemple prouvant que, si

, le fait que
 \geq Sp(v))
n'implique pas nécessairement que
)
.
3) Soient
)
. Montrer l'équivalence des conditions suivantes :
i)
 \geq Sp(v))
ii) Il existe
)
(l'ensemble des endomorphisme orthogonaux) tel que

(

est l'adjoint de

)
Voilà, la seule chose que j'ai réussi à faire c'est le contre-exemple (quand même), c'est à dire la question 2.b. La première question je vois pas du tout comment trouver l'inf et le sup. Le calcul est facile pour les vecteurs propres séparés, mais rien ne me dit qu'en prenant une combinaison linéaire de ces vecteurs, je ne peux pas obtenir quelque chose de plus petit ou de plus grand. En faisant le calcul avec un vecteur quelconque
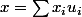
j'obtiens
)}{(x,x)} = \frac{\sum a_i x_i^2 (u_i,u_i)}{\sum x_i^2 (u_i,u_i)})
ce qui m'avance pas plus que ça...
Les questions 2.a et 3 sont typiquement des questions que je ne sais pas par quel bout prendre.
Merci d'avance de votre aide !
