Bonjour,
je doit étudier la convergence de la suite définie par
Un=(1/n²)*somme(de K=1 à n) des E(Kx)
(désolé pour la notation)
Je fait une étude pour x apartenant à ]-inf;0[u[1;+inf)
Je trouve que la suite tent vers E(x).
Ensuite je doit étudié la suite pour 0<=x<1 :
Mais, je ne vois pas comment m'y prendre.
Merci de votre aide.
Problème sur des suites
11 messages
- Page 1 sur 1
Non la question c'est juste d'étudier la convergence
Dans mon idée:
Je sortais K de E(kx) car K apartient à N.Je m'étais E(x) en facteur de la somme. Je développe la somme
J'optenais:
E(x)*(1/n²)*((n(n+1)/2)que je simplifié
=E(x)(n+1)/n
=E(x)(n/n)(1+1/n)/1)
=E(x)(1+1/n)
Et ca tend vers E(x)
Par contre si x compris entre 0 et 1, je ne peux pas sortir K de E(Kx) car: par exemple (petite démonstration par l'absurde :lol3: )
Si x=0.01, E(x)=0 => K*E(x)=0
mais Si K=100 et X=0.01 => E(K*x)=E(100*0.01)=E(1)=1
C'est pour ca que j'ai séparé l'étude.
Dans mon idée:
Je sortais K de E(kx) car K apartient à N.Je m'étais E(x) en facteur de la somme. Je développe la somme
J'optenais:
E(x)*(1/n²)*((n(n+1)/2)que je simplifié
=E(x)(n+1)/n
=E(x)(n/n)(1+1/n)/1)
=E(x)(1+1/n)
Et ca tend vers E(x)
Par contre si x compris entre 0 et 1, je ne peux pas sortir K de E(Kx) car: par exemple (petite démonstration par l'absurde :lol3: )
Si x=0.01, E(x)=0 => K*E(x)=0
mais Si K=100 et X=0.01 => E(K*x)=E(100*0.01)=E(1)=1
C'est pour ca que j'ai séparé l'étude.
yo,
ptite boulette ici :we: (ca vaut qqch comme n(n+1)/2)
On peut faire ca pour<kx)
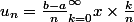
avec a=0, et b=1 et dire que c'est une somme de riemann cqui est équivalent avec n qui tend vers linfini à l'intégrale
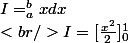
et dire avec convergence normale que pour tout x dans [0;1[ vu que E(kx)<E(k*1) et E(k*1) converge alors ca u_n(x) aussi
;) de 1 à n de k = n.
ptite boulette ici :we: (ca vaut qqch comme n(n+1)/2)
On peut faire ca pour
avec a=0, et b=1 et dire que c'est une somme de riemann cqui est équivalent avec n qui tend vers linfini à l'intégrale
et dire avec convergence normale que pour tout x dans [0;1[ vu que E(kx)<E(k*1) et E(k*1) converge alors ca u_n(x) aussi
la vie est une fête 
d'ou u(n) < x/n.
Il devient alors évident que lim u(n) =0.
en réécrivant ton inégalité correctement, on a
u_n< x/n^2(n^2+n)/2
et en l'infini
u_n<x/2
on ne sait pas dire que ca converge vers x/2 (a la rigueur on veut juste montrer que ca converge donc c'est good), juste que ca converge avant x/2. pour montrer que c précisément x/2, faudrait encadrer u_n de lautre coté avec ta méthode.
la vie est une fête 
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
