Pour information je connais
On demande de prouver que f est sol de (E) si et seulement si h=f-g est sol de
f sol de (E)
f sol de (E)
A partir de là je bloque. Merci d'avance.
Equation différentielle
4 messages
- Page 1 sur 1
Equation différentielle
par thibaut47500 » 13 Jan 2011, 17:33
Bonjour à tous, je bloque sur une démonstration d'équation différentielle.
Pour information je connais=4exp^{-2x})
qui est une sol de (E).
:y'=-3y+4exp^{-2x})
On demande de prouver que f est sol de (E) si et seulement si h=f-g est sol de:y'=-3y)
.
f sol de (E)
f sol de (E))
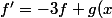A partir de là je bloque. Merci d'avance.
Pour information je connais
On demande de prouver que f est sol de (E) si et seulement si h=f-g est sol de
f sol de (E)
f sol de (E)
A partir de là je bloque. Merci d'avance.
par Vahngal » 13 Jan 2011, 17:38
thibaut47500 a écrit:Bonjour à tous, je bloque sur une démonstration d'équation différentielle.
Pour information je connais
On demande de prouver que f est sol de (E) si et seulement si h=f-g est sol de
f sol de (E)
f sol de (E)
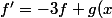A partir de là je bloque. Merci d'avance.
Il faut partir de h=f-g solution de (E')...
par Vahngal » 13 Jan 2011, 18:06
thibaut47500 a écrit:Notre prof nous conseille de toujours partir de la gauche.
En fait le "si et seulement si" veut dire :
* si f solution de (E) alors h solution de (E') (implication)
et
* si h solution de (E') alors f est solution de (E) (réciproque)
En clair tu as équivalence des deux affirmations ( h solution de (E') f solution de (E) )
Içi, il est plus judicieux de partir de h solution de (E') et raisonner par équivalence.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :