Intégrale et suite

[colas]

bonjour un peu d'aide ne serait pas de refus

Soit la suite Un= Intégrale (x+1)e^(-x) dx de n à n+1

1) montrer l'existence de la suite U=(Un)
2) A l'aide d'une IPP calculer Un en fonction de n
3) Etudier la convergence de la suite U.
4) pour tout entier n on pose Sn = somme (de i=0 à i=n) Ui
a) calculer sn en fonction de n et determiner la limite de la suite Sn

Pour la 2 je trouve Un = (n+2)e^(-n) - (n+3)e^-(n+1) par contre je n'arrive pas a etudier sa convergence.
Pour la 4 je trouve Sn = -(n+3)e^-(n+3) +2 par contre je n'arrive pas a etudier sa convergence.

Merci de votre aide

[fred]

Je suis d'accord sur le 2)

[Mikou]

Pour la 2 je trouve Un = (n+2)e^(-n) - (n+3)e^-(n+1) par contre je n'arrive pas a etudier sa convergence : si tu le sais parfaitement.

[fred]

Ton résultat du 2 peut s'écrire
Un= (1-1/e) n exp(-n) + (2-3/e) exp(-n)
or lim n exp(-n) en + infini=0
de même lim exp(-n) en + infini =0
donc lim Un quand n tend vers infini=0

[Neeb]

Faux, je cherche encore !

[Huit]

Salut, je veux pas dire de bétise mais :

*
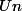
est décroissante, tu as du savoir le démontrer.

*

Or et
Donc

Un est donc décroissante et minorée, elle est donc convergente

[fred]

Tu as trouvé Sn = -(n+3)e^-(n+3) +2
N'est ce pas plutot Sn = -(n+3)e^-(n+1) +2

[fred]

qqsoit k<>0 lim x^k exp(x)=0 quand x tend vers -infini
or Sn = -(n+3)e^-(n+1) +2= 2 - (n+1) e^-(n+1) - 2 e^-(n+1)
donc lim Sn en +infini =2