Estimation d'une somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
The Void
- Membre Relatif
- Messages: 187
- Enregistré le: 25 Mar 2007, 20:33
-
 par The Void » 03 Jan 2011, 19:04
par The Void » 03 Jan 2011, 19:04
Bonjour,
Je cherche à donner un equivalent (ou O) simple de:
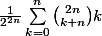
quand

En majorant k par n, on trouve un O(n), mais je suis presque sûr que c'est O(
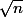
), savez vous comment le démontrer? (j'ai pensé à une inégalité du type Hoeffding mais bof..)
-
geegee
- Membre Rationnel
- Messages: 799
- Enregistré le: 11 Mai 2008, 13:17
-
 par geegee » 03 Jan 2011, 21:21
par geegee » 03 Jan 2011, 21:21

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Jan 2011, 23:59
par Ben314 » 03 Jan 2011, 23:59
Salut,
Si
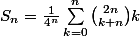
alors
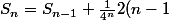\choose n-1} =\cdots=\sum_{m=0}^{n-1} \frac{1}{4^{m+1}}{2m\choose m})
et on doit trouver une bonne approximation en utilisant le fait que

(stirling)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
The Void
- Membre Relatif
- Messages: 187
- Enregistré le: 25 Mar 2007, 20:33
-
 par The Void » 04 Jan 2011, 10:57
par The Void » 04 Jan 2011, 10:57
Ben314 a écrit: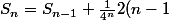\choose n-1})
Comment trouves tu cette égalité?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Jan 2011, 11:03
par Ben314 » 04 Jan 2011, 11:03
En regardant d'un peu plus prés, on a :

donc

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Jan 2011, 11:08
par Ben314 » 04 Jan 2011, 11:08
The Void a écrit:Comment trouves tu cette égalité?
En utilisant le fait que

puis en multipliant par
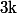
et en sommant de
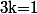
à
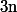
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités