Une petite Factorisation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 21:47
par Foudesmathss » 03 Jan 2011, 21:47
Bonsoir, cela fait un jours que je n'arrive pas à faire la factorisation:
3-12(x-1)²
J'ai essayé de factoriser par 3 : 3(1-4)(x-1)² mais apres je ne sais plus quoi faire. On m'a suggéré une identité remarquable mais je ne la vois pas.
Merci d'avance.
-
Anonyme
 par Anonyme » 03 Jan 2011, 21:50
par Anonyme » 03 Jan 2011, 21:50
bonsoir,
l'identité remarquable est (a-b)²= a²-2ab+b²
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 21:52
par Foudesmathss » 03 Jan 2011, 21:52
Mais à quelle parenthèse s'applique t'elle ? Si j'essaie, ça donne:
3-12(x-1)²
=3(1-4)(x-1)²
= 3(1-4)(x²-2x+1) Est ce juste ?
Que faire ensuite ?
-
Anonyme
 par Anonyme » 03 Jan 2011, 21:56
par Anonyme » 03 Jan 2011, 21:56
Bonsoir,
3-12(x-1)² = 3(1-4(x-1)²) = 3((-3)(x-1)²) = -9(x-1)²
Pourquoi développer ? :)
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Jan 2011, 21:58
par Jimm15 » 03 Jan 2011, 21:58
Bonsoir,
Attention ! Vous soustrayez des éléments sans tenir compte des multiplications (prioritaires, pour rappel).
^2=3\left[1-4(x-1)^2\right])
.
À partir de là, utilisez légalité remarquable
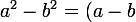(a+b))
dans le crochet.
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 21:59
par Foudesmathss » 03 Jan 2011, 21:59
Je ne sais pas, j'ai vu la réponse d'un de mes camarades et elle me semblait juste, elle ressemblait à 3 ( ...) (...)
-
Anonyme
 par Anonyme » 03 Jan 2011, 21:59
par Anonyme » 03 Jan 2011, 21:59
Foudesmathss a écrit:Mais à quelle parenthèse s'applique t'elle ? Si j'essaie, ça donne:
3-12(x-1)²
=3(1-4)(x-1)²
= 3(1-4)(x²-2x+1) Est ce juste ?
Que faire ensuite ?
non!
sa te donne:
3-12(x²-2x+1)= ?
-
Anonyme
 par Anonyme » 03 Jan 2011, 21:59
par Anonyme » 03 Jan 2011, 21:59
Ah oui, c'est vrai, j'avais pas vu l'erreur. Je suis bête.
Applique la méthode de Jimmy :)
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 22:00
par Foudesmathss » 03 Jan 2011, 22:00
Mais Faut t'il appliquer l'identité remarquable sur 1-4 ou sur (x-1)² ?
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 22:02
par Foudesmathss » 03 Jan 2011, 22:02
Cela me donne donc, 3[( 1-4)(x-1)²]
= 3(1-2)(1+2)(x-1)²
-
Anonyme
 par Anonyme » 03 Jan 2011, 22:03
par Anonyme » 03 Jan 2011, 22:03
Regarde :
3[1-4(x-1)²] = 3[1²-(2(x-1))²]
Tu vois l'identité remarquable ? ;)
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Jan 2011, 22:08
par Jimm15 » 03 Jan 2011, 22:08
Foudesmathss a écrit:Cela me donne donc, 3[( 1-4)(x-1)²]
= 3(1-2)(1+2)(x-1)²
Encore une fois, vous ne respectez la priorité des opérations.
Vous
ne pouvez pas écrire que
^2=(1-4)(x-1)^2)
car le 1 nest pas multiplié à
^2)
!! En effet,
^2=1-4\times (x-1)^2=1-\left(4(x-1)^2\right))
.
Remarque :
Si cétait le cas, on aurait (x-1)^2=(x-1)^2-4(x-1)^2) ...
...Remarquez que
^2\right]=3\left[1^2-2^2 (x-1)^2 \right]=3\left[1^2-\left (2(x-1) \right )^2 \right])
puis utilisez légalité remarquable.
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 22:08
par Foudesmathss » 03 Jan 2011, 22:08
Ah oui, Merci, je vois.
Cela donne donc 3[ 1-(2(x-1)) (1+(2(x-1))]
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 22:12
par Foudesmathss » 03 Jan 2011, 22:12
Et pour résultat final, je trouve 3(3-2x)(3+2x) Est ce juste ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Jan 2011, 22:13
par Jimm15 » 03 Jan 2011, 22:13
Foudesmathss a écrit:Ah oui, Merci, je vois.
Cela donne donc 3[ 1-(2(x-1)) (1+(2(x-1))]
Faites bien attention aux parenthèses :
\right] \left[1+2(x-1)\right] \right])
.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Jan 2011, 22:15
par Jimm15 » 03 Jan 2011, 22:15
Foudesmathss a écrit:Et pour résultat final, je trouve 3(3-2x)(3+2x) Est ce juste ?
Non.
La première parenthèse est juste mais pas la seconde.
Faites attention lors du développement de
)
.
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 22:17
par Foudesmathss » 03 Jan 2011, 22:17
Excusez Moi.
C'est bien 3[(3-2x)(2x-1)] ?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 03 Jan 2011, 22:18
par Jimm15 » 03 Jan 2011, 22:18
Foudesmathss a écrit:Excusez Moi.
C'est bien 3[(3-2x)(2x-1)] ?
Oui, cest exact.
-
Foudesmathss
- Membre Naturel
- Messages: 22
- Enregistré le: 06 Mar 2010, 16:30
-
 par Foudesmathss » 03 Jan 2011, 22:23
par Foudesmathss » 03 Jan 2011, 22:23
Je vous remercie tous pour votre aide précieuse sans laquelle je n'aurai jamais compris cette factorisation. Maintenant, je saurai factoriser les expressions de ce type. Encore une fois, Merci et bonne année à vous.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
