Suite extraite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yoo
- Membre Naturel
- Messages: 23
- Enregistré le: 02 Aoû 2006, 13:45
-
 par yoo » 02 Jan 2011, 16:40
par yoo » 02 Jan 2011, 16:40
bonjour , je bloque sur la question suivante : comment je peux démontrer que la suite x(n)= (0,0,....,1,0,....) .[1 à la n eme place 0 partout] n'admet pas de suite extraite qui converge . cordialement
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 02 Jan 2011, 16:55
par girdav » 02 Jan 2011, 16:55
Bonjour,
on se place dans quel espace?
-
yoo
- Membre Naturel
- Messages: 23
- Enregistré le: 02 Aoû 2006, 13:45
-
 par yoo » 02 Jan 2011, 17:02
par yoo » 02 Jan 2011, 17:02
oula j'ai oublié de préciser on travaille dans l^p: c' est l'ensemble des suites réelles x=(xi) telles que la serie de terme général (la valeur absolue de xi)^p converge
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 02 Jan 2011, 17:04
par girdav » 02 Jan 2011, 17:04
Tu peux calculer la distance entre deux termes distincts de la suite.
-
yoo
- Membre Naturel
- Messages: 23
- Enregistré le: 02 Aoû 2006, 13:45
-
 par yoo » 02 Jan 2011, 17:42
par yoo » 02 Jan 2011, 17:42
ahh oui je vois :lol3: . tu veux montrer qu'aucune sous suite ne peut être de Cauchy et puisqu'on est dans un espace complet on peut conclure . pour la norme sur l^p je choisi quoi comme norme pour faire le calcul je sais qu'elles sont tout équivalente .
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 02 Jan 2011, 17:46
par girdav » 02 Jan 2011, 17:46
S'il est dit "sur
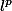
" avec

alors on est obligé de prendre la norme
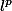
:
^{\fr 1p})
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
