je bloque sur une question, la dernière de mon devoir.j'ai:
et je dois montrer que:
je n'y arrive pas du tout, alors merci d'avance pour toute aide ! :we:
Demontrer egalite
6 messages
- Page 1 sur 1
demontrer egalite
par Daewin » 02 Jan 2011, 12:07
bonjour,
je bloque sur une question, la dernière de mon devoir.j'ai:
=\frac{-\sqrt(R)+exp(i\Delta\phi)}{1-\sqrt(R)exp(i\Delta\phi)})
et je dois montrer que:
=\frac{1+\sqrt(R)}{1-\sqrt(R)}(tan(\frac{\Delta\phi}{2})))
je n'y arrive pas du tout, alors merci d'avance pour toute aide ! :we:
je bloque sur une question, la dernière de mon devoir.j'ai:
et je dois montrer que:
je n'y arrive pas du tout, alors merci d'avance pour toute aide ! :we:
par X4nth3 » 02 Jan 2011, 14:53
Bonjour ,
je n'ai pas fait le calcul mais je pense que peux t'en sortir en utilisant les formules d'Euler : = \frac{ e^{i \theta}+e^{-i \theta}}{2})
et  = \frac{ e^{i \theta}-e^{-i \theta}}{2i})
et les formules suivantes , qui sont juste de la trigo classique  =\frac{1-t^2}{1+t^2})
et  =\frac{2t}{1+t^2})
où on a posé )
Essaye de mélanger un peu ça et à mon avis , tu devrais trouver ton résultat.
je n'ai pas fait le calcul mais je pense que peux t'en sortir en utilisant les formules d'Euler :
Essaye de mélanger un peu ça et à mon avis , tu devrais trouver ton résultat.
par X4nth3 » 03 Jan 2011, 11:28
Salut ,
je suis désolé mais j'avais pas eu le temps de chercher. Enfin , je crois que j'ai la solution.
Alors d'abord je pose)
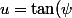et )
.
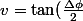En utilisant la formule d'Euler , l'expression de départ se reécrit :
 +i \sin(2 \psi) = \frac{ -\sqrt(R) + \cos(\Delta \phi) + i \sin(\Delta \phi)}{1- \sqrt(R)(\cos(\Delta \phi) + i \sin(\Delta \phi))})
Ensuite , on introduit
et
On obtient :
(1+v^2)+1-v^2+2iv}{1+v^2-\sqrt(R)(1-v^2+2iv)})
(Ici j'ai déjà un peu simplifié)
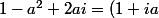Bon ensuite on remarque que^2)
Donc
^2}{1+u^2} = \frac{-\sqrt(R)(1+v^2)+(1+iv)^2}{1+v^2-\sqrt(R)(1+iv)^2})
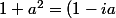et on remarque enfin que(1+ia))
ce qui te permet de simplifier les deux membres.
Tu devrais pouvoir finir.J'ai pas été beaucoup plus loin mais tout s'arrange tellement bien qu'à mon humble avis ça doit marcher.
N'oublie pas qu'on veut arriver à}{1-\sqrt(R)} v)
je suis désolé mais j'avais pas eu le temps de chercher. Enfin , je crois que j'ai la solution.
Alors d'abord je pose
En utilisant la formule d'Euler , l'expression de départ se reécrit :
Ensuite , on introduit
Bon ensuite on remarque que
et on remarque enfin que
Tu devrais pouvoir finir.J'ai pas été beaucoup plus loin mais tout s'arrange tellement bien qu'à mon humble avis ça doit marcher.
N'oublie pas qu'on veut arriver à
par Daewin » 03 Jan 2011, 13:07
merci pour cette énorme coup de pouce ! ne reste plus qu'à compléter et finir :lol3:
merci !
merci !
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :