soit
Comment montrer que la fonction admet un minimum global? J'ai essayé de trouver un point critique mais sans succès...
Optimisation
3 messages
- Page 1 sur 1
optimisation
par lisonn » 31 Déc 2010, 10:43
Bonjour
soit= x^4 -2x^3 +3(x^2+y^2) -5(x+y) +4xy)
.
Comment montrer que la fonction admet un minimum global? J'ai essayé de trouver un point critique mais sans succès...
soit
Comment montrer que la fonction admet un minimum global? J'ai essayé de trouver un point critique mais sans succès...
par fatal_error » 31 Déc 2010, 12:12
yo,
alors, le but, c'est de faire apparaitre une signature positive, ca serait cool.
=x^4-2x^3+3x^2+3y^2-5x-5y+4xy\\<br />f(x,y)=(x^2-x)^2-x^2+3x^2+3y^2-5x-5y+4xy\\<br />a=(x^2-x)^2\\<br />f(x,y)=a+2x^2+3y^2-5x-5y+4xy\\<br />f(x,y)=a+2(x - (\frac{5}{4} - y))^2 - 2( (\frac{5}{4} - y)^2+3y^2-5x-5y+4xy\\<br />b=2(x - (\frac{5}{4} - y))^2\\<br />f(x,y)=a+b+3y^2-5y-2(\frac{25}{16}+y^2 - \frac{5}{2}y)\\<br />f(x,y)=a+b+y^2- \frac{25}{8}\\<br />f(x,y)=a+b+c-\frac{25}{8}\\)
avec
donc on peut minorer f par
Apres, on peut ptet dire que vu qu'elle est minorée elle admet un minimum, mais jme rappele plus des théorêmes XD
alors, le but, c'est de faire apparaitre une signature positive, ca serait cool.
avec
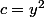
donc on peut minorer f par
Apres, on peut ptet dire que vu qu'elle est minorée elle admet un minimum, mais jme rappele plus des théorêmes XD
la vie est une fête 
par lisonn » 31 Déc 2010, 15:24
Oulala, je voyais pas ca aussi compliqué^^. Je vais me pencher sur les calculs, merci de la réponse.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :