Comment trouver la dérivée
17 messages
- Page 1 sur 1
Comment trouver la dérivée
Bonjour, Je sais que j'ai deja mis un message similaire mais il y en avait tellement que je ne comprennait plus la conversation ...
Je dois calculer la dérivée de f(x) = Ln ( 2 - (2 / x+3) ) pour x = -1
Donc :
f(-1) = 2 - (2/-1+3)
f'(-1) = 0
g(-1) = Ln
g'(-1) = 1 / x POUR g J'AI UN DOUTE et c'est donc la que j'ai besoin d'aide :s
mais donc si c'est juste ça donnerai f'(-1) x g'(f(-1))
donc 0 x ( 1 / Ln ) = 0
Je dois calculer la dérivée de f(x) = Ln ( 2 - (2 / x+3) ) pour x = -1
Donc :
f(-1) = 2 - (2/-1+3)
f'(-1) = 0
g(-1) = Ln
g'(-1) = 1 / x POUR g J'AI UN DOUTE et c'est donc la que j'ai besoin d'aide :s
mais donc si c'est juste ça donnerai f'(-1) x g'(f(-1))
donc 0 x ( 1 / Ln ) = 0
Salut,
Non ce n'est pas du tout ça, il faut dériver f pour trouver l'expression de f'(x) puis l'évaluer pour x = -1.
Ce que tu as écris est totalement faux car lorsque je remplace x par une valeur en particulier, f(x) donne toujours un nombre ! Donc si l'on raisonne comme tu viens de le faire toutes les dérivées seraient nulles.
Ton g sort de nulle part, en regardant ton autre topic j'ai vu que tu as introduis des fonction composée dans ce cas tu en a 2 et f reste la fonction globale.
Si tu veux introduire les fonctions composée il faut en introduire deux, par exemple g et h et écrire que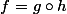
Non ce n'est pas du tout ça, il faut dériver f pour trouver l'expression de f'(x) puis l'évaluer pour x = -1.
Ce que tu as écris est totalement faux car lorsque je remplace x par une valeur en particulier, f(x) donne toujours un nombre ! Donc si l'on raisonne comme tu viens de le faire toutes les dérivées seraient nulles.
Ton g sort de nulle part, en regardant ton autre topic j'ai vu que tu as introduis des fonction composée dans ce cas tu en a 2 et f reste la fonction globale.
Si tu veux introduire les fonctions composée il faut en introduire deux, par exemple g et h et écrire que
Oui ca donne bien ça pour l'expression de )
Maintenant plutôt que d'introduire l'écriture de f sous la forme de deux fonctions composées et risquer de se tromper, on peut se rappeler que pour u fonction de x,
]' = \frac{u'}{u})
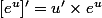

etc ...
En gros tu prends la dérivée de la fonction classique que tu connais déjà à savoir]' = \frac{1}{x})
et lorsque tu remplaces x par u, il faut multiplier l'expression par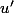 et on obtient
et on obtient ]' = \frac{u'}{u})
Donc ici si on a = ln(2-\frac{2}{x+3})) ,
,
 = \frac{\left(2-\frac{2}{x+3}\right)'}{2-\frac{2}{x+3}})
Maintenant plutôt que d'introduire l'écriture de f sous la forme de deux fonctions composées et risquer de se tromper, on peut se rappeler que pour u fonction de x,
etc ...
En gros tu prends la dérivée de la fonction classique que tu connais déjà à savoir
et lorsque tu remplaces x par u, il faut multiplier l'expression par
Donc ici si on a
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
