Symétrie point repère vecteur

par **Mallaury38** » 27 Déc 2010, 17:14

Je n'arrive pas à trouver la méthode pour trouver la réponse à cette question.
Mon calcul me permet de trouver la réponse juste (je l'ai vérifié en regardant mon graphique) mais je ne suis pas sure qu'il soit correct.
Pouvez-vous m'aider s'il vous plaît ?
Voici l'énoncé et la question:

Dans un repère on donne les points:
I(4;1), K(-1;3) et A(6;3)

a) A' est l'image de A par la symétrie de centre I, et A'' et l'image de A' par la symétrie de centre K.
Calculer les coordonnées de A', puis celles de A''.
Placer les points.

Merci !

par **oscar** » 27 Déc 2010, 17:41

Bonjour

V AI ( -2;-2)=> VA'I=( 4;1)+(-2;-2) = ( 2;-1)

Idem pour A" => (-2;...

Trace une figure

par **Mallaury38** » 27 Déc 2010, 19:19

oscar a écrit:Bonjour

V AI ( -2;-2)=> VA'I=( 4;1)+(-2;-2) = ( 2;-1)

Idem pour A" => (-2;...

Trace une figure

Merci alors apparement mon calcul était juste mais je ne l'ai pas tout à fait rédigé pareil:

{xA'= xI+xIA'
{yA'= yI+yIA'
{xA'=4+(-2)
{yA'=1+(-2)
{xA'=2
{yA'=-1

En tout cas merci bien :we:

par **Mallaury38** » 28 Déc 2010, 14:12

Par contre comment procède-t-on pour A" ?

par **XENSECP** » 28 Déc 2010, 14:16

Mallaury38 a écrit:Par contre comment procède-t-on pour A" ?

De façon analogue vu que tu as aussi une symétrie centrale

par **Mallaury38** » 28 Déc 2010, 14:52

XENSECP a écrit:De façon analogue vu que tu as aussi une symétrie centrale

Oui merci j'ai donc trouvé A"(-4;7)

En revanche je ne trouve pas la dernière question.
J'ai réussi à prouver que les vecteurs IK et AA" sont colinéaires (question b) mais la question c je n'y arrive pas.

c) Plus généralement, reprendre les questions a) et b) avec A(x;y) I(a;b) et K (a';b').
Quelle propriété de géométrie vient-on de retrouver.

par **XENSECP** » 28 Déc 2010, 14:54

Ah bah tu remplaces dans tes calculs numériques les coordonnées des points par des lettres.... Si tu as compris ce que tu as fait précédemment normalement c'est pas plus compliqué !

par **Mallaury38** » 28 Déc 2010, 14:59

XENSECP a écrit:Ah bah tu remplaces dans tes calculs numériques les coordonnées des points par des lettres.... Si tu as compris ce que tu as fait précédemment normalement c'est pas plus compliqué !

C'est ce que j'ai commencé à faire mais au début du calcul pour trouver les coordonnées de A' je me retrouve avec

xA'= a+ a-x
yA'= b+ b-y

Et à ce moment là je crois qu'i lfaut faire xA'=x et yA'=y mais je ne n'en suis pas sûre car dans mes calculs les coordonnées de A ne sont pas égales à celles de A'

par **XENSECP** » 28 Déc 2010, 15:03

Mallaury38 a écrit:
a) A' est l'image de A par la symétrie de centre I

En gros ça veut dire que :

Après tu remplaces l'expression vectorielle par des coordonnées !

par **Mallaury38** » 28 Déc 2010, 15:09

XENSECP a écrit:En gros ça veut dire que :

Après tu remplaces l'expression vectorielle par des coordonnées !

Ok merci

par **Mallaury38** » 28 Déc 2010, 16:22

C'est certainement stupide mais je n'y arrive toujours pas :triste:

par **Mallaury38** » 29 Déc 2010, 14:34

XENSECP a écrit:En gros ça veut dire que :

Après tu remplaces l'expression vectorielle par des coordonnées !

Je n'y arrive toujours pas je dois tout compliquer car je me retrouve avec des calculs vraiment impossible.

par **Mallaury38** » 29 Déc 2010, 15:46

Quelqu'un peut-il m'aider svp ?

par **Mortelune** » 29 Déc 2010, 16:02

Mallaury38 a écrit:Dans un repère on donne les points:
I(x;y), K(k;l) et A(a;b)

a) A' est l'image de A par la symétrie de centre I, et A'' et l'image de A' par la symétrie de centre K.
Calculer les coordonnées de A', puis celles de A''.
Placer les points.

Si j'ai bien compris tu bloques sur ça (j'ai juste changer le nom des coordonnées de K).
Pour s'aider on peut déjà noter : A'(a',b') et A"(a",b") ça peut permettre de décomposer les calculs.

Comme il l'a été précisé plus haut on va utiliser des vecteurs, on aura besoin de :

,

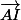
ainsi que de a' et b'.

On cherche A' tel que

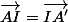
et A" tel que

.

Normalement ça dégrossit la difficulté.

par **Mallaury38** » 29 Déc 2010, 16:18

Du coup les coordonnées de A'(x;y) et celles de A"(k;l)
Donc après A'K(k-x ; l-y) et KA"(k-k; l-l) ?

par **Mortelune** » 29 Déc 2010, 16:34

Tu es en train de dire que A'=I et A"= K sur ta première ligne, ce qui implique A=I et donc I=A=K, ou alors tu as encore changé de notations.

Essaye d'exprimer AI, a', b' et A'K avec les notations que j'ai utilisé.

par **Mallaury38** » 29 Déc 2010, 17:49

J'ai un petit soucis car avec A ( a;b) I(x;y) et AI=IA' AI(a-x; b-y)

Ce qui me donne :

xA'= xI+ xIA'
yA'=yI+yIA'

xA'=x+a-x
yA'=y+b-y

xA'=a
yA'=b

par **Mortelune** » 29 Déc 2010, 17:54

C'est parce que IA'=AI=(x-a,y-b) ;)

par **Mallaury38** » 29 Déc 2010, 17:54

Ah bas oui bien sûr !
Pardon

par **Mallaury38** » 29 Déc 2010, 18:03

Et après avoir
A'( 2x-a ; 2y-b) et A"(2k-2x-a ; 2l-2y-b)

Ainsi que le vecteur IK( k-x ; l-y ) et AA"(2k-2x-2a; 2l-2y-2b)
Que dois-je faire ?

Symétrie point repère vecteur

Symétrie point repère vecteur

Qui est en ligne