Equation fonctionelle (3)
Olympiades mathématiques, énigmes et défis
-
Anonyme
 par Anonyme » 27 Déc 2010, 21:09
par Anonyme » 27 Déc 2010, 21:09
Soit

tel que
=f(n+m^2))
pour tout
)
de
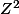
.
Bon travail.
-
Anonyme
 par Anonyme » 28 Déc 2010, 13:25
par Anonyme » 28 Déc 2010, 13:25
Personne n'est intéressé ? Je l'ai trouve assez intéressante (pour un débutant comme moi en tout cas :marteau: )
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 28 Déc 2010, 13:35
par vincentroumezy » 28 Déc 2010, 13:35
Il y'a des solutions à cette "quatio onctionnelle, je n'aurais pas cru ?
-
Anonyme
 par Anonyme » 28 Déc 2010, 13:46
par Anonyme » 28 Déc 2010, 13:46
Déjà les fonctions constantes sont des solutions triviales. Mais sont elles les seules ? that is the question :lol3:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 28 Déc 2010, 14:02
par vincentroumezy » 28 Déc 2010, 14:02
Je crois que ce sont les seuls, mais il faut le démontrer.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 28 Déc 2010, 15:25
par girdav » 28 Déc 2010, 15:25
Bonjour,
en remplaçant m par -m on obtient que pour tous

et

on a
 = f(m+n^2))
donc en particulier
 = f(1+m))
. En faisant n=0 dans l'équation de départ on a
=f(m^2))
donc
 = f((-m)^2) =f(-m))
donc on a que
=f(m+2))
pour tout

.

est donc entièrement déterminée par
)
et
)
. Réciproquement, vu que

et

ont toujours la même parité on voit que toute fonction telle que
 =1)
et
 =1)
convient.
-
Anonyme
 par Anonyme » 28 Déc 2010, 15:32
par Anonyme » 28 Déc 2010, 15:32
girdav a écrit:donc
 = f((-m)^2) =f(-m))
faute de frappe ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 28 Déc 2010, 17:21
par girdav » 28 Déc 2010, 17:21
Oui je voulais bien sûr dire que
=f(m))
pour tout

. Je vais la laisser pour que ton message garde son sens (ou alors les modérateurs vont mettre tout ça en ordre).
-
Anonyme
 par Anonyme » 28 Déc 2010, 17:27
par Anonyme » 28 Déc 2010, 17:27
Il y a aussi un souci dans la 1ere ligne : en remplaçant m par -m on n'obtient pas cette expression.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 28 Déc 2010, 17:30
par girdav » 28 Déc 2010, 17:30
Qmath a écrit:Il y a aussi un souci dans la 1ere ligne : en remplaçant m par -m on n'obtient pas cette expression.
 = f((-m)^2+n) =f(m^2+n) = f(m+n^2))
, non?
-
Anonyme
 par Anonyme » 28 Déc 2010, 17:32
par Anonyme » 28 Déc 2010, 17:32
girdav a écrit: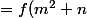 = f(m+n^2))
, non?
pourquoi ?
-
Malo
- Membre Naturel
- Messages: 33
- Enregistré le: 29 Oct 2010, 16:50
-
 par Malo » 28 Déc 2010, 17:36
par Malo » 28 Déc 2010, 17:36
Excusez-moi, ma question est peut-être "bête", mais pourquoi a-t-on le droit, comme ça, de remplacer m par (-m) dans l'équation ?
-
Anonyme
 par Anonyme » 28 Déc 2010, 17:37
par Anonyme » 28 Déc 2010, 17:37
En effet :mur:
Belle demo , assez courte comparé a la mienne qui utilise une récurrence forte .
Aussi je ne suis pas sur d'avoir compris la notation que tu utilise vers la fin avec la #.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 28 Déc 2010, 17:38
par girdav » 28 Déc 2010, 17:38
Parce que si

alors

.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 28 Déc 2010, 17:39
par girdav » 28 Déc 2010, 17:39
Qmath a écrit:En effet :mur:
Belle demo , assez courte comparé a la mienne qui utilise une récurrence forte .
Aussi je ne suis pas sur d'avoir compris la notation que tu utilise vers la fin avec la #.
C'est le cardinal (j'aurais peut-être du mettre

).
-
Anonyme
 par Anonyme » 28 Déc 2010, 17:44
par Anonyme » 28 Déc 2010, 17:44
girdav a écrit:C'est le cardinal (j'aurais peut-être du mettre

).
cardinal comme celui qu'on utilise pour les ensemble ? si oui je vois mal ce qu'il viens faire ici.
On passe a une autre équation ? :zen: ( j'ai une assez originale par contre je l'ai pas encore resolu ) ça tintéresse ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 28 Déc 2010, 18:01
par girdav » 28 Déc 2010, 18:01
Qmath a écrit:cardinal comme celui qu'on utilise pour les ensemble ? si oui je vois mal ce qu'il viens faire ici.
On passe a une autre équation ? :zen: ( j'ai une assez originale par contre je l'ai pas encore resolu ) ça tintéresse ?
C'est juste pour dire que tous les nombres pairs ont la même image ainsi que tous les nombres impairs.
Amène donc l'originale !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
 et
et  on a
on a  = f(m+n^2)) donc en particulier
donc en particulier  = f(1+m)) . En faisant n=0 dans l'équation de départ on a
. En faisant n=0 dans l'équation de départ on a =f(m^2)) donc
donc  = f((-m)^2) =f(-m)) donc on a que
donc on a que =f(m+2)) pour tout
pour tout  .
.  est donc entièrement déterminée par
est donc entièrement déterminée par ) et
et ) . Réciproquement, vu que
. Réciproquement, vu que  et
et  ont toujours la même parité on voit que toute fonction telle que
ont toujours la même parité on voit que toute fonction telle que  =1) et
et  =1) convient.
convient.