Dérivation 1ere S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Flobobo
- Membre Naturel
- Messages: 96
- Enregistré le: 26 Oct 2010, 17:53
-
 par Flobobo » 28 Déc 2010, 15:41
par Flobobo » 28 Déc 2010, 15:41
Bonjour, j'aimerai de l'aide pour une question sur les dérivations s'il vous plaît:
f est définie par f(x)=
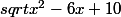
Montrer que le taux de variation au voisinage de 3 peut s'écrire:
-f(3)}{h}=\frac{h}{sqrt{h^2+1}+1})
J'ai donc commencé à développer :
-f(3)}{h}=\frac{sqrt{(3+h)^2-6*(3+h)+10}-sqrt{9-6*3+10}}{h})
J'arrive à :
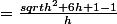
Une fois ici je bloque, je ne sais vraiment pas comment faire, quelqu'un pourrait-il m'aider svp ?
Merci d'avance
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Déc 2010, 15:49
par Sylviel » 28 Déc 2010, 15:49
multiplie et divise par la quantité conjuguée.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Flobobo
- Membre Naturel
- Messages: 96
- Enregistré le: 26 Oct 2010, 17:53
-
 par Flobobo » 28 Déc 2010, 15:51
par Flobobo » 28 Déc 2010, 15:51
Par le quantité conjuguée ?
-
Euler07
- Membre Irrationnel
- Messages: 1157
- Enregistré le: 25 Avr 2009, 11:00
-
 par Euler07 » 28 Déc 2010, 15:53
par Euler07 » 28 Déc 2010, 15:53
Le conjugué de a+b est a-b
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Déc 2010, 15:53
par Sylviel » 28 Déc 2010, 15:53
la quantité conjuguée de
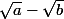
est
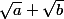
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Flobobo
- Membre Naturel
- Messages: 96
- Enregistré le: 26 Oct 2010, 17:53
-
 par Flobobo » 28 Déc 2010, 16:04
par Flobobo » 28 Déc 2010, 16:04
Ok merci donc ici ce que je dois faire c'est:
*(sqrt{h^2+6h+1}+sqrt{1})}{sqrt{h^2+6h+1}+sqrt{1}})
?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 28 Déc 2010, 18:34
par Sylviel » 28 Déc 2010, 18:34
Oui, et si tu pousses un tout petit peu le calcul tu va comprendre pourquoi !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Flobobo
- Membre Naturel
- Messages: 96
- Enregistré le: 26 Oct 2010, 17:53
-
 par Flobobo » 28 Déc 2010, 18:52
par Flobobo » 28 Déc 2010, 18:52
J'en arrive à:
^2}-sqrt{1}}{h*sqrt{h^2+6h+1}+h})
Une fois ici je ne sais pas comment je pourrais supprimer le numérateur
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 29 Déc 2010, 11:30
par Sylviel » 29 Déc 2010, 11:30
La racine d'un carré ça ne te dis rien ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Flobobo
- Membre Naturel
- Messages: 96
- Enregistré le: 26 Oct 2010, 17:53
-
 par Flobobo » 29 Déc 2010, 13:07
par Flobobo » 29 Déc 2010, 13:07
Si bien sur, mais ca ne m'avance pas plus en fait:
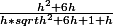
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 29 Déc 2010, 14:33
par XENSECP » 29 Déc 2010, 14:33
Flobobo a écrit:J'ai donc commencé à développer :
-f(3)}{h}=\frac{sqrt{(3+h)^2-6*(3+h)+10}-sqrt{9-6*3+10}}{h})
J'arrive à :
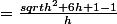
En fait ça c'est faux déjà...
C'est plutôt
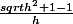
.
La conclusion est ensuite immédiate (conjugué, simplification des h et c'est gagné).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
