Postion de Cf par rapport à T
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Pasqua
- Membre Naturel
- Messages: 78
- Enregistré le: 24 Avr 2006, 14:10
-
 par Pasqua » 03 Mai 2006, 14:55
par Pasqua » 03 Mai 2006, 14:55
Bonjour amis matheux,
On me demande d'etudier la postion de Cf courbe representatif de f(x), fonction definie sur R par 2x+1/x²+x+1par rapport à sa tangente T.
L'equation de T est y = x
Je décide donc d'etudier le signe de la difference.
J'obtiens -x^3-x²-x+1/x²+x+1
Pouvez vous me corriger ?
Aussi si c'est juste coment etudier le signe de -x^3+x ?
Merci d'avance.
-
pafab
- Membre Naturel
- Messages: 23
- Enregistré le: 01 Mai 2006, 23:48
-
 par pafab » 03 Mai 2006, 14:56
par pafab » 03 Mai 2006, 14:56
l'usage des parenthèses n'est pas facultatif!!!! surtout en maths!!!
ce qui rend la lecture de tes formules difficile car différemment intreprétable
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 03 Mai 2006, 14:58
par fonfon » 03 Mai 2006, 14:58
Salut, ce nest pas juste il faut bien etudier le signe de la difference sauf que
}=f(x)-x=\frac{(2x+1)}{x^2+x+1}-x=\frac{-x^3-x^2+x+1}{x^2+x+1})
reverifie
-
pafab
- Membre Naturel
- Messages: 23
- Enregistré le: 01 Mai 2006, 23:48
-
 par pafab » 03 Mai 2006, 14:59
par pafab » 03 Mai 2006, 14:59
doit on lire f(x) = (2x+1)/(x²+x+1)?
Dans ce cas, je ne vois pas comment tu trouves (-x^3+x)/(x²+x+1)...
-
pafab
- Membre Naturel
- Messages: 23
- Enregistré le: 01 Mai 2006, 23:48
-
 par pafab » 03 Mai 2006, 15:01
par pafab » 03 Mai 2006, 15:01
cool la réponse est toute faite...
pour le signe de -x^3-x²+x+1, il faut chercher une racine évidente x0 et factoriser en (x -x0)(ax²+bx+c) puis étudier les signes, aprèd avoir déterminé a,b et c.
-
pafab
- Membre Naturel
- Messages: 23
- Enregistré le: 01 Mai 2006, 23:48
-
 par pafab » 03 Mai 2006, 15:02
par pafab » 03 Mai 2006, 15:02
on peut aussi essayer de factoriser directement -x^3-x² et faire apparaître un facteur commun.
-
Pasqua
- Membre Naturel
- Messages: 78
- Enregistré le: 24 Avr 2006, 14:10
-
 par Pasqua » 03 Mai 2006, 15:28
par Pasqua » 03 Mai 2006, 15:28
pafab a écrit:on peut aussi essayer de factoriser directement -x^3-x² et faire apparaître un facteur commun.
j'ai trouvé 1 et -1 en racine evidente, je factorise par l'un des deux ?
-
Pasqua
- Membre Naturel
- Messages: 78
- Enregistré le: 24 Avr 2006, 14:10
-
 par Pasqua » 03 Mai 2006, 15:38
par Pasqua » 03 Mai 2006, 15:38
si oui je trouve (x+1)(-x²+1)
-
pafab
- Membre Naturel
- Messages: 23
- Enregistré le: 01 Mai 2006, 23:48
-
 par pafab » 03 Mai 2006, 16:04
par pafab » 03 Mai 2006, 16:04
la réponse est oui!!
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 03 Mai 2006, 16:05
par fonfon » 03 Mai 2006, 16:05
Salut, la factorisation est
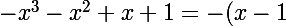\times(x+1)^2)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
