Calcul d'une intégrale (version 2.0)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 26 Déc 2010, 18:29
par leofonte » 26 Déc 2010, 18:29
Bonsoir,
J'ai décidé de réviser un peu avant les partiels ( ben oui un peu quand même...) et je suis tombé sur des annales avec une intégrale que je n'aime pas trop.
La voici
Intégrale de 1 à x de (t+1)/(t(t-1/e)) dt
Quelqu'un peut-il m'aider?
Merci d'avance
Léo
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Déc 2010, 19:14
par girdav » 26 Déc 2010, 19:14
Bonjour,
as-tu essayé une décomposition en éléments simples?
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 26 Déc 2010, 20:12
par leofonte » 26 Déc 2010, 20:12
J'ai tenté en vain...
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 26 Déc 2010, 20:25
par Arnaud-29-31 » 26 Déc 2010, 20:25
Salut,
T'as pas du tenté longtemps ... ca te donne quoi la décomposition en éléments simples ?
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 26 Déc 2010, 21:56
par sad13 » 26 Déc 2010, 21:56
Oui à part la décomposition en éléments simples, rien ne m'inspire mais peux tu l'écrire en latex ou plus clairement car j'ai du mal à voir le "e" , il est avec qui?
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 26 Déc 2010, 22:24
par leofonte » 26 Déc 2010, 22:24
}dt)
Wouah ça vaut le coup de lire un tuto sur le latex!
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 27 Déc 2010, 00:11
par leofonte » 27 Déc 2010, 00:11
Effectivement ce n'était vraiment pas dur.
Merci pour toutes les réponses. Je le dis à chaque fois mais, super forum!
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 27 Déc 2010, 10:22
par sad13 » 27 Déc 2010, 10:22
Ben voilà finalement, tu l'as conclu avec .... décomposition en éléments simples
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 27 Déc 2010, 13:46
par leofonte » 27 Déc 2010, 13:46
Me revoilà avec un autre problème...
L'intégrale principale est F(x)=

On nous propose d'abord de la résoudre en calculant (par une intégration par parties)

et d'en déduire F(x)
J'ai trouvé

Là encore je ne suis pas sûr du résultat. On nous propose ensuite de calculer F(x) d'une seconde manière, en effectuant un changement de variable
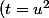)
Et je sèche, quelqu'un peut-il m'aider?
Merci d'avance

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Déc 2010, 13:55
par Ericovitchi » 27 Déc 2010, 13:55
déjà la première est simple, elle s'écrit

Pour la seconde partie, effectivement fait une intégration par partie en l'écrivant
 d(\sqrt{t}))
Et effectivement ça donne
)/sqrt(t) dt = 2/3 \sqrt{x} (x-3 ln(x)+6)-14/3)
C'est à peu près la même chose sauf que j'ai -14/3 à la place de ton -5/3
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 27 Déc 2010, 14:08
par leofonte » 27 Déc 2010, 14:08
Oui j'avais confondu un -1 avec un -4... Je vais tenter pour le changement de variable. Merci beaucoup ;)
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 27 Déc 2010, 14:14
par leofonte » 27 Déc 2010, 14:14
Je tourne en boucle avec le changement de variable. Je ne comprend l'aide que ça m'apporte...
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 27 Déc 2010, 14:23
par leofonte » 27 Déc 2010, 14:23
Ericovitchi a écrit:déjà la première est simple, elle s'écrit

Pour la seconde partie, effectivement fait une intégration par partie en l'écrivant
 d(\sqrt{t}))
Et effectivement ça donne
)/sqrt(t) dt = 2/3 \sqrt{x} (x-3 ln(x)+6)-14/3)
C'est à peu près la même chose sauf que j'ai -14/3 à la place de ton -5/3
Je ne comprend pas le
 d(\sqrt{t}))
. Comment avez vous obtenu cela?
-
leofonte
- Membre Naturel
- Messages: 30
- Enregistré le: 26 Sep 2010, 12:12
-
 par leofonte » 27 Déc 2010, 16:05
par leofonte » 27 Déc 2010, 16:05
J'ai réussi en trouvant un cours sur les changements de variable. Il me manquait les bases!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités

 et d'en déduire F(x)
et d'en déduire F(x)
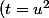)
