Calcul exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 15:35
par fordson65 » 26 Déc 2010, 15:35
bonjour à tous,
voila j'ai un petit problème de calcul:
j'ai préalablement démontré que:

jusque là tout va bien mais on me demande d'en déduire que:
^n)
quelque chose doit m'échapper car ce n'est que du calcul mais je bloque!!
merci d'avance!
sinon pour une precision: estce que
^n=e)
????? :marteau:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 26 Déc 2010, 16:19
par Sylviel » 26 Déc 2010, 16:19
Est-ce que tu as montré ta première inégalité pour un n réel ? (qu'on écris en général x).
Pourrais tu l'appliquer à 1/n ? :lol3:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 16:24
par fordson65 » 26 Déc 2010, 16:24
oui en effet ja'i pour la premiere inegalité pour tt x appartenant a R
pour la deuxieme : pour tt n appartenant à N*
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 26 Déc 2010, 16:29
par Arnaud-29-31 » 26 Déc 2010, 16:29
Salut,
On montre facilement que l'exponentielle est convexe, si je prends sa tangente en un point, elle est tjrs située au dessus de sa tangente.
Ici si je prends la tangente en x=0 à la courbe représentative de la fonction

, l'équation de cette tangente est
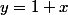
et on a bien

comme tu l'as déjà démontré.
Maintenant si j'élève cette inégalité à la puissance n avec

j'ai
^n \hspace{5} \forall x \in \mathbb{R})
Et en posant
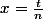
,
^n \hspace{5} \forall t \in \mathbb{R})
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 16:38
par fordson65 » 26 Déc 2010, 16:38
merci bcp pour ta réponse même si la méthode me parait un peu bizarre !!
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 26 Déc 2010, 16:45
par Arnaud-29-31 » 26 Déc 2010, 16:45
Qu'est-ce qui te paraît bizarre ? :s
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 16:56
par fordson65 » 26 Déc 2010, 16:56
j'ai bien compris la démarche mais moi et les changements de variables ca fait deux!!
pour aller plus loin j'aimerais démontrer la convergeance de
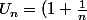^n)
vers e mais en feuilletant mon livre je ne trouve pas grand chose qui puisse m'aider?
pourrait tu me guider?? ca me parait difficile avec mes quelques notions sur les limites!!
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 26 Déc 2010, 18:21
par Arnaud-29-31 » 26 Déc 2010, 18:21
Utilise la forme exponentielle-log
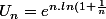} = e^{\frac{ln(1+\frac{1}{n})}{\frac{1}{n}}})
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 18:26
par fordson65 » 26 Déc 2010, 18:26
la ca ne m'aide pas vraiment en fait...
je ne connait pas le log neperien
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 18:38
par fordson65 » 26 Déc 2010, 18:38
la limite m'est difficile à determiner en + l'infinie.
il y aurait il une methode miracle??
autant pour moi j'ai la solution dans le livre merci beaucoup pour ton aide!!
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 26 Déc 2010, 18:54
par sad13 » 26 Déc 2010, 18:54
salut, avant tout : pour répondre à ta dernière question ; c'est faux
.(\frac{e^n}{n})^n=e : revois le cours.
ensuite, t'es en terminale je présume donc la convexité c'est hors sujet et en remplaçant n apr 1/n t'as répondu à la question.
ensuite , pour ta question sur la convergence de Un vers e , peux préciser les outils que vous avez car étant donén que t'as pas le log, t'as donc pas que : a^b=exp(b*lna), donc où tu vas conjecturer ou bien en passant par les suites récurrentes ou bien je serai tenté d'utiliser les théorèmes des gendarmes car si c'est à la suite de ta première inégalité, c'est qu'il y a ,quand même , un certain lien.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 26 Déc 2010, 19:14
par Arnaud-29-31 » 26 Déc 2010, 19:14
L'étude des fonctions convexes avec la "vraie" définition est bien sûr hors programme, mais en terme de vocabulaire, un élève de terminale sait expliquer avec les mains ce que veut dire convexe ou concave (il vaut mieux pour reconnaître les miroirs en optique).
Donc repérer que le 1+x représente l'équation de la tangente en zéro et remarquer que vu la tronche de l'exponentiel, elle est tjrs au dessus de sa tangente est une bonne chose pour illustrer le problème.
Maintenant bien sur pour le démontrer proprement au niveau de terminale, on étudie par exemple la fonction e^x - x - 1
-
fordson65
- Membre Naturel
- Messages: 96
- Enregistré le: 04 Fév 2009, 19:16
-
 par fordson65 » 26 Déc 2010, 19:45
par fordson65 » 26 Déc 2010, 19:45
non en réalité il n'y a pas de lien parce que le dm ne pose pas la question (on se contente du minimum)
donc voila c'était pour vérifier que la suite converge bien vers e
merci pour vos réponses et une fois de plus ce forum est génial (enfin le forum en lui même n'est rien sans ses membres expérimentés)
bonne fin de soirée!
-
sad13
- Membre Irrationnel
- Messages: 1526
- Enregistré le: 29 Oct 2010, 21:37
-
 par sad13 » 26 Déc 2010, 20:02
par sad13 » 26 Déc 2010, 20:02
Ok ben dans ce cas là, l'outil pr une classe de term c'est le log et la méthode d'Arnaud est la plus élégante .
de rien et bonne soirée, gardes ce résultat en tête , tu le verras en cours d'année
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités