Identité de Vandermonde
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 21 Déc 2010, 17:39
par Cryptocatron-11 » 21 Déc 2010, 17:39
Bonsoir,
En cherchant à démontrer l'identité de Vandermonde, j'ai eu besoin d'utiliser cette formule (produit de polynômes):
 x^{k})
mais je ne la comprends pas pourrais je avoir un petit développement pour y voir plus clair ?
c'est surtout

que je ne comprends pas. je ne vois pas comment on le met de cette forme là.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 21 Déc 2010, 17:43
par girdav » 21 Déc 2010, 17:43
Bonjour,
on a
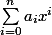\(\sum_{j=0}^mb_jx^j\)= \sum_{i=0}^n\sum_{j=0}^ma_ib_jx^{i+j})
puis on regroupe suivant les valeurs de
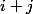
. Si

alors
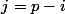
.
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 21 Déc 2010, 17:48
par Cryptocatron-11 » 21 Déc 2010, 17:48
girdav a écrit: Si

alors
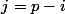
.
ah oui bien vu ! merci
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 22 Déc 2010, 10:47
par arnaud32 » 22 Déc 2010, 10:47
ca suppose cependant de donner un sens a a_j pour j>n et b_j pour j>0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités