Un déterminant

[girdav]

Bonjour,
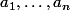
on se donne nombres complexes et on note pour entier .
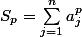
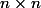
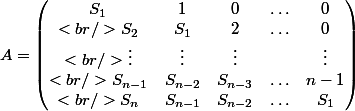
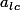
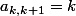
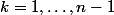
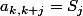
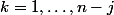
On considère la matrice de taille , autrement dit, en notant le terme de la ligne et de la colonne : (), () et ailleurs.
Que vaut ?

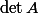
[Ben314]

Salut,
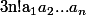
Sauf erreur ça fait et je pense que ça se déduit assez façilement des formules de Newton (à vérifier...)

[girdav]

Oui, je trouve la même chose et de la même manière.

[Ben314]

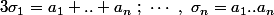
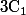
Si on note les polynômes symétriques, il suffit d'ajouter à la colonne la quantité pour la rendre entièrement nulle sauf le terme du bas qui vaut .
On développe par rapport à cette colonne et on a le résultat.

[girdav]

Oui, on a presque l'impression que ce déterminant est fait pour appliquer les formules de Newton. Je vais regarder si on peut faire sans, c'est-à-dire avec d'autres combinaisons que celle-là.