Statistiques faciles?

par **laura.f** » 20 Déc 2010, 12:11

bonjour à tous, voila je suis en pleine revision de mes partiels mais je bloque sur un exercice de statistiques!
voila l'énoncé:

soit l'évolution du prix d'un produit en fonction des années, donnée par le tableau suivant:

Années : xi Prix (euros) : yi
1982 4
1983 X
1984 9
1985 14
1986 20
Calculer le prix en 1983, sachant que le coefficient directeur de la droite des moindres carrés est de 3,8
J'ai essayé plusieurs methodes mais rien n'aboutit a un resultat valable! merci

par **fabular** » 20 Déc 2010, 14:09

Bonjour,

Je ne sais pas quelle est ta formation en statistique.

Si tu as l'habitude du modèle linéaire, écris ton modèle de régression comme un modèle linéaire en explicitant bien la matrice de design

et le vecteur des paramètres de la droite de régression

.

Tu as alors que l'estimateur optimal doit vérifier :

(c'est la formule classique pour calculer les paramètres de la droite de régression, elle définit l'estimateur des moindres carrés)

Ce qui dans ton cas te donne un système de deux équations à deux inconnues. Sauf que dans le cas de l'exercice, les inconnues ne sont pas les paramètres de pente et d'ordonnée à l'origine contenus dans

mais le paramètre d'ordonnée à l'origine et une valeur observée.

Cela reste un système que tu peux résoudre pour trouver à la fois la valeur X manquante (je trouve 10) et l'ordonnée à l'origine (je trouve -0.4).

Si tu n'as pas l'habitude de manipuler le modèle linéaire, si ce n'est pas à ton programme ou s'il te faut plus d'explications, n'hésite pas !

Bon courage !

par **laura.f** » 20 Déc 2010, 17:51

merci beaucoup mais je t'avoue je ne comprend pas grand chose!
nous avons juste etudier la formule des moindre carrée et dans les precedant exercices que j'ai étudié nous remplacons les années par des indices (1,2,3...)
quelle est l'equation à deux inconnus que tu trouves?

par **fabular** » 21 Déc 2010, 12:44

Je pense pas que ça te servirait à grand chose d'avoir mon système pour rédiger une solution à ton exercice. Le risque c'est que la méthode utilisée plus haut n'ait rien à voir avec ce qu'on vous a appris.

On va faire autrement :

- effectivement on peut remplacer les années par des indices, ça ne change rien et c'est plus facile pour les calculs

- Normalement ta formule des moindres carrés doit ressembler à ça :

où
*

est la pente de la droite de régression
*

est l'ordonnée à l'origine de la droite de régression
*

est la valeur de l'année pour la i-eme observation donc comme on a remplacé les années par des indices on a directement

*

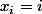
est la valeur du prix pour la i-ème observation, donc tu connais tous les

sauf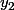

qui est ton inconnue X !!

- si dans cette formule tu remplaces le paramètre de la pente de la droite de régression, qui est d'habitude une inconnue, par 3,8, alors tu dois obtenir un système d'équations à deux inconnues : la valeur X que tu cherches et l'ordonnée à l'origine de ta droite

.

Reste plus qu'à résoudre !

par **laura.f** » 21 Déc 2010, 16:30

en faite voila ma seule et unique formule:
sigma (xi-x(barre))(yi-y(barre)) / sigma (xi-x(barre))
autant te dire que le reste c'est du chinois!
tu avait trouvé quelle prix pour 1893?
en tout cas merci beaucoup de m'aider!

par **fabular** » 21 Déc 2010, 18:38

La formule que tu viens de poster est l'expression du coefficient directeur de ta droite régression en fonction des années (xi) et des prix (yi).

Or on te dit que ce coefficient directeur vaut 3.8. Tu as donc une équation :

sigma (xi-x(barre))(yi-y(barre)) / sigma (xi-x(barre)) = 3.8

La seule inconnue dans cette équation est y2=X !

Il suffit donc de résoudre cette équation à une inconnue. Je pense que de là tu peux terminer.

par **laura.f** » 21 Déc 2010, 20:43

je suis désolé je ne comprend pas cette equation!
d'ou sort le y2 et le 3,8 est passé ou?!
merci beaucoup tu m'es d'une grande aide!

par **fabular** » 22 Déc 2010, 01:29

On s'est mal compris : quand je disais y2=X je voulais juste dire que y2 c'est X, il s'agit de ton inconnue, à savoir le prix observé à la deuxième année. Et tu peux calculer ce y2 en résolvant l'équation :

sigma (xi-x(barre))(yi-y(barre)) / sigma (xi-x(barre)) = 3.8

qui est une simple équation à une inconnue puisque tu connais toutes les autres variables.

par **laura.f** » 23 Déc 2010, 10:34

oui j'avais bien compris, mais en ce qui concerne je n'ai aucune information sur xbarre et ybarre et je n'ai aucun moyen de le calculer n'ayant pas la valeure de X

par **fabular** » 23 Déc 2010, 14:43

Rhooo tu dramatises un petit peu là :D :
- xbarre c'est par définition la moyenne empirique des xi : (x1+x2+x3+x4+x5)/5, donc comme tu connais tous les xi tu peux le calculer !
- ybarre c'est par définition la moyenne empirique des prix yi : (y1+y2+y3+y4+y5)/5. Or effectivement tu ne connais pas y2 (= X), qui est ton inconnue. Mais tu peux quand même exprimer ybarre en fonction de X.

Si tu remplace xbarre par sa valeur numérique et ybarre par son expression en fonction de X dans la grande équation :

sigma (xi-x(barre))(yi-y(barre)) / sigma (xi-x(barre)) = 3.8

tu vas bien obtenir une équation avec X comme unique inconnue que tu peux résoudre !

par **laura.f** » 23 Déc 2010, 17:25

hey donc en faite la j'arrive a (2-3)(yi-ybarre)=3,8
en faite j'arrive pas a sortir le Y barre donc mon equation n'avance pas!

par **fabular** » 23 Déc 2010, 17:37

xbarre = (x1+x2+x3+x4+x5)/5 = (1+2+3+4+5)/5
ybarre = (y1+y2+y3+y4+y5)/5 = (4+X+9+14+20)/5
donc tu peux faire avancer ton équation...
D'autre part désolé mais j'avais pas vu avant, il y a une erreur dans ta formule, il manque un carré au dénominateur (vérifie dans ton cours) ! La grosse équation à résoudre c'est donc :

sigma (xi-x(barre))(yi-y(barre)) / sigma ((xi-x(barre))^2) = 3.8

par **laura.f** » 23 Déc 2010, 17:43

oui j'avais remarqué l'érreur!
donc pour y barre je trouve 9,4+X
X barre = 3
Xi=2

reponse de l'equation = 7,1 cets juste?

par **fabular** » 23 Déc 2010, 18:03

hihi non pas tout à fait :
ybarre = 9.4+X/5
xbarre = 3 c'est bon

sinon qu'est ce que tu appelles Xi ?

faut que tu refasses le calcul :langue2: !

par **laura.f** » 23 Déc 2010, 18:07

pour moi xi c'est le rang de l'année x la 2
j'ai refais le calcul je trouve 25,9 cela me parait faux

par **fabular** » 23 Déc 2010, 18:41

Mmh ça me semble pas très clair tout ça ! Alors non pour être précis, xi c'est l'indice de l'année i.

Est-ce que tu as bien compris le sens du sigma dans ta formule ?
Si je réécris sans la notation sigma l'équation à résoudre, sommes-nous bien d'accord que l'équation c'est :
((y1-ybarre)(x1-xbarre)+(y2-ybarre)(x2-xbarre)+...+(y5-ybarre)(x5-xbarre)) /
((x1-xbarre)^2+ (x2-xbarre)^2+...+(x5-xbarre)^2))= 3.8

?

Sinon je t'invite à réviser la notation sigma, qui permet d'éviter d'écrire explicitement des sommes (ici des sommes pour i allant de 1 à 5).

par **laura.f** » 24 Déc 2010, 19:08

Oui ne t'inquite pas j'ai bien compris la signification de sigma c'est juste que au niveau des y il y a un problemes car plusieurs inconnues et une seule equation..

par **fabular** » 25 Déc 2010, 10:26

laura.f a écrit:Oui ne t'inquite pas j'ai bien compris la signification de sigma c'est juste que au niveau des y il y a un problemes car plusieurs inconnues et une seule equation..

Non non, tu connais tous les variables en "y" sauf :
- y2 qui vaut X
- ybarre qui vaut 9.4+X/5
Mais tu as donc bien qu'une seule inconnue dans ton équation, c'est X.

Joyeux noël

!

Statistiques faciles?

Statistiques faciles?

Qui est en ligne