Limite d'une fonction en un point de R

[ludo56]

Bonjour,en regardant un peu la litterature, je me suis aperçu qu'il y avait deux definitions différentes de la limite en un point fini de :
La limite pointé et la limite epointé.
Dans un bouquin,j'ai vu une définition qui englobe les deux précedentes,il s'agit de la limite suivant une partie de (Par exemple la limite en de la fonction si different de et si vaut suivant la partie privé de et n'existe pas sur la partie .
Ici,on voit bien que la limite dépend de la partie choisie.
J'ai alors deux questions:
1)Dans le cas ou on choisit deux parties differentes A et B ne contenant pas a (cas ou à l'adhérence de la partie privée de la partie),alors la limite dépend t'elle de la partie choisie?
2)Je suis preneur de toutes subtilité et commentaire la dessus!

[windows7]

salut,

1) c'est clair non ?
2) bah enfait la seule subtilité c'est que ya une definition qui donne rien, et la seconde qui propose une limite.

[ludo56]

Si c'était clair pour moi je poserais pas la question..

[windows7]

par exemple

on prend f(0)=0 f(x)= 0.5 si x dans Q+* f(x)=1 si x dans iR+

c'est quoi la limite de f en 0 suivant Q*+ ? c'est quoi la limite de f suivant iR+ ?

(iR = irrationels )

[ludo56]

Il faut que je m'absente une petite heure désolé.J'y réfléchirai en rentrant!

[Ben314]

Salut,
Pour ta question 1), il me semble que le cas archi classique où on calcule la "limite à droite" et la "limite à gauche" répondent clairement à ta question : il est trés façile de trouver des exemples où ces deux limites existent mais ne coïncident pas.

Pour la question 2), c'est un peu "métaphisico-machin chose" comme question.
Le seul truc, c'est, si tu est étudiant avec un prof., d'essayer de t'en tenir à la définition qu'a choisi le prof (et de faire gaffe lorsque tu pioche des exos à droite à gauche que ce soit bien la même qui est prise).
Si t'as pas de prof., ben... tu fait juste gaffe... :zen:

[ludo56]

D'accord donc la limite suivant Q+* est 1/2 et la limite suivant R+* est 1. Donc la limite dépend de la partie choisie,merci à vous deux.
Du coup,comment définir la limite à gauche et à droite? (vu qu'elles dépendent des parties choisies)
Moi je l'ai definit ainsi:On dit que f admet une limite à droite en a si f admet une limite en a suivant la partie A inter]a,+oo[. Le problème,c'est que cette limite dépend de la partie A choisit donc comment appeler cette limite à droite?
Merci

[Ben314]

D'accord donc la limite suivant Q+* est 1/2 et la limite suivant R+* est 1. Donc la limite dépend de la partie choisie,merci à vous deux.
Du coup,comment définir la limite à gauche et à droite? (vu qu'elles dépendent des parties choisies)

Merci

Ben non, par définition, la limite à droite en xo, c'est la limite suivant la partie (en supposant bien sûr que cette partie n'est pas vide.

Bon, sinon ton truc concernant "la limite suivant Q+* est 1/2 et la limite suivant R+* est 1" est clairement incohérent : si une partie A est contenue dans une partie B (par exemple Q+* est contenu dans R+*) et que la limite suivant B existe alors forcément celle suivant A existe aussi et vaut la même chose : il suffit d'écrire les deux définitions pour voir que celle avec B implique celle avec A !

[windows7]

ben > c'est pas IR+ mais iIR + ( irrationels positifs ) qu'il fallait lire ..

[Ben314]

ben > c'est pas IR+ mais iIR + ( irrationels positifs ) qu'il fallait lire ..

Je pense que R\Q serait plus adapté comme notation...

[ludo56]

Oui en fait je voulais dire la limite suivant iR+* ,j'ai oublié le i,merci.

[ludo56]

[quote="Ben314"]Ben non, par définition, la limite à droite en xo, c'est la limite suivant la partie (en supposant bien sûr que cette partie n'est pas vide.
QUOTE]
Es tu certains? Ne peut-on pas parler de limite à gauche ou à droite suivant des parties (genre A inter ]-oo,a[ avec A inclus dans Df et a \in à l'adhérence de A)?
Sinon comment écrire le théorème qui dit que la limite suivant une partie A en a existe ssi la limite à gauche et à droite existent et coincident ?

[ludo56]

Par exemple soit la fonction f définit par:
f(x)=1/2 si à
si

Alors la limite a droite et à gauche en 0 suivant la partie iR est 1/2 et la limite à droite et à gauche suivant la partie Q* est 1
La limite sur n'existe pas mais la limite suivant vaut
La limite suivant vaut 1

[Ben314]

Bon, je le redit, je pense que de noter iR les irrationnels, c'est quand même un peu con : par rapport à R\Q, ça économise UN caractère... et par contre, ça va à l'encontre de la notation archi classique concernant les groupes, anneaux, espaces vectoriels, etc qui dit que aX, c'est l'ensemble des éléments de la forme ax où x décrit X. Donc iR, pour n'importe quel matheux, ça peut désigner qu'un seul truc, c'est les éléments de la forme ix où x décrit R.

Concernant les limites à droite et à gauche, oui, je suis totalement sûr de moi :
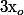
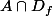
Pour toute partie A de R telle que soit dans l'adhérence de on définit la "limite suivant A" que l'on note en général puis, comme on l'utilise un peu plus souvent que le reste, on définit 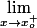comme étant un "racourci" pour
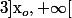
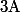
Si tu veut autre chose que comme ensemble , ben tu revient à la notation de départ.

Quand à la preuve du résultat dont tu parle, il suffit d'écrire les trois définitions (limite à droite, limite à gauche et limite "épointée") pour voir qu'il y a équivalence.

[ludo56]

Merci mais je dois admettre que beaucoup de choses me chagrinent encore. J'ai du mal à admettre qu'à partir du moment ou on définit la limite sur une partie,on ne puisse pas parler de limite à droite et à gauche sur cette partie (cela revient a considerer la limite à droite et à gauche de la restriction de f sur cette partie) C'est ce que j'ai fais dans le poste précédent.
Voila,sinon je suis d'accord avec toi pour la notation R\Q.

[Doraki]

Parler de limite selon une partie ça permet déjà de parler de limite à gauche ou à droite.

Si une partie A de Df admet un réel a dans son adhérence, on peut définir la notion de limite en a de f|A.

A partir de là on peut éviter de parler de limite "à gauche" ou "à droite" vu que c'est des cas particuliers qu'on obtient en prenant des parties A particulières.


Le théorème dont tu veux parler serait un truc du genre :

Si A1 et A2 sont deux parties de Df ayant le réel a dans leur adhérence, et si les limites en a de f|A1 et de f|A2 existent et sont les mêmes, alors la limite en a de f|(A1 union A2) existe (et vaut la même chose que les deux autres limites)

Si A1 et A2 sont deux parties de Df ayant le réel a dans leur adhérence, si A1 contient A2, et si la limite en a de f|A1 existe, alors la limite en a de f|A2 existe (et vaut la même chose que l'autre limite)

[ludo56]

Oui c'est bien à ce genre de truc que je pensais..Merci à toi!