dans un exercice on s'est donné une fonction
Il s'agit de montrer que la suite
Une piste pour le démonter ?? Le TAF ne permet pas de conclure ...
Etude d'une suite
7 messages
- Page 1 sur 1
Etude d'une suite
par euler21 » 19 Déc 2010, 19:37
Bonsoir
dans un exercice on s'est donné une fonction
à valeur strictement positive de classe C1 telle que }{\phi (x)} \sim \frac{\alpha}{x})
à l'infini où 
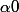
Il s'agit de montrer que la suite}{\phi (n)} -1))
est bornée.
Une piste pour le démonter ?? Le TAF ne permet pas de conclure ...
dans un exercice on s'est donné une fonction
Il s'agit de montrer que la suite
Une piste pour le démonter ?? Le TAF ne permet pas de conclure ...
par windows7 » 19 Déc 2010, 19:58
salut,
ton expression c'est aussi n* ( (phi(n+1)-phi(n) )/phi(n)) , si tu vois ce que je veux dire :lol3:
ton expression c'est aussi n* ( (phi(n+1)-phi(n) )/phi(n)) , si tu vois ce que je veux dire :lol3:
par euler21 » 19 Déc 2010, 22:02
Salut
En suivant ton raisonnement, puisque est de classe C1 il existe un 
compris entre n et n+1 tel que  - \phi (n) = \phi ' (c_n))
après je ne sais plus quoi faire, d'autant que la fonction est croissante (
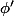
a un signe positif à partir d'un certain rang) :triste:
Que faire ??
En suivant ton raisonnement, puisque
Que faire ??
par Ben314 » 19 Déc 2010, 23:19
Salut
P'tète que tu pourrait écrire que - \phi (n)}{\phi(n)} = \frac{\phi ' (c_n)}{\phi(n)}= \frac{\phi ' (c_n)} {\phi(c_n)}\times\frac{\phi(c_n)} {\phi(n)})
...
P'tète que tu pourrait écrire que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Doraki » 20 Déc 2010, 10:07
Moi j'partirais plutôt de ;)(n+1) - ;)(n) <= ;)(n+1)*A/n pour un certain A, et voir ce qu'on peut faire avec.
par arnaud32 » 20 Déc 2010, 11:14
Puis que  = \frac{\alpha \Phi(t)}{t}(1+o(1)))
pour t assez grand > 0)
et 
est croissante
-\Phi(n)=\int _n^{n+1}\Phi '(t)dt)
pour n assez grand et avec 0<a<1/2
}{\Phi(n)}-1)| = |n*\int _n^{n+1}\frac{\Phi '(t)}{\Phi(n)}dt| = \alpha*\int _n^{n+1}\frac{n}{t}\frac{\Phi(t)}{\Phi(n)}(1+ \epsilon (t))dt \leq \alpha*\int _n^{n+1}\frac{n}{t}\frac{\Phi(t)}{\Phi(n)}(1+ a)dt)
car est positive et  =0)
comme est croissante
}{\Phi(n)}-1)| \leq \alpha\frac{\Phi(n+1)}{\Phi(n)}(1+ a))
de plus tu as
}{\Phi(t)}dt| \leq (1+a)\alpha \ln(\frac{n+1}{n}))
donc}{\Phi(n)}) \leq (1+a)\alpha \ln(\frac{n+1}{n}))
et pour n assez grand}{\Phi(n)} \leq K)
avec
pour t assez grand
pour n assez grand et avec 0<a<1/2
car
comme
de plus tu as
donc
et pour n assez grand
7 messages
- Page 1 sur 1
Qui est en ligne
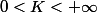
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :