Equation différentielle non linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 16 Déc 2010, 22:25
par benekire2 » 16 Déc 2010, 22:25
bonsoir a tous !
Je cherche a résoudre sur R+ l'équation diff : y'=-0.013y²+9.81 (pour la physique) et j'ai trouvé les solutions générales en fonction d'une solution particulière ( ricatti)
Mais comment obtenir une solution particulière ? Ou au moins sa forme ?
Merci à vous !
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 17 Déc 2010, 00:01
par Arnaud-29-31 » 17 Déc 2010, 00:01
Salut,
Il s'agit de résoudre

... ca me fait penser à quelques epsilons près un une formule de trigo célèbre ... Non ?? ^^
On peut clairement s'attendre à voir du tangente hyperbolique en solution.
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
 par JeanJ » 17 Déc 2010, 07:20
par JeanJ » 17 Déc 2010, 07:20
Variables séparables :
dy/(-0.013y²+9.81) = dx
-
Black Jack
 par Black Jack » 17 Déc 2010, 10:16
par Black Jack » 17 Déc 2010, 10:16
D'accord avec JeanJ.
Mais si tu veux vraiment une solution particulière, y = V(9,81/0,013) devrait faire l'affaire.
:zen:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 17 Déc 2010, 14:10
par benekire2 » 17 Déc 2010, 14:10
Merci a tous , finalement , j'ai pu me démerder :zen:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 18 Déc 2010, 00:55
par Arnaud-29-31 » 18 Déc 2010, 00:55
Je post quand même pour le plaisir ^^
On veut résoudre


, ca fait beaucoup penser a tanh (

)
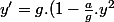)
On pose

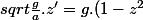)
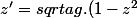)
Ici on propose donc
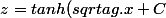)
Et
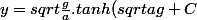)
-
Black Jack
 par Black Jack » 18 Déc 2010, 10:51
par Black Jack » 18 Déc 2010, 10:51
Ou autrement :
y' = b - ay² (avec a et y > 0)
dy/(b-ay²) = dx
dy/((b/a)-y²) = a dx
(1/2).V(a/b).[1/(V(b/a)-y) + 1/(V(b/a)+y)] dy = a dx
(1/2).V(a/b).ln|K.(V(b/a)+y)/(V(b/a)-y)| = a.x
K.(V(b/a)+y)/(V(b/a)-y) = e^(2x.V(ab))

Avec K une constante réelle.
:zen:
-
grikor
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Mai 2009, 16:39
-
 par grikor » 18 Déc 2010, 12:53
par grikor » 18 Déc 2010, 12:53
Bonjour
une solution particulière y=27.47027
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
 par JeanJ » 18 Déc 2010, 14:21
par JeanJ » 18 Déc 2010, 14:21
Dans le cas d'équation non-linéaire, une solution particulière ne sert pas à grand chose, pour ne pas aller jusqu'à dire que ça ne sert à rien (Peut-être pour une vérification à-postériori, lorsqu'on a trouvé la solution sans s'en servir ? )
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 18 Déc 2010, 16:09
par benekire2 » 18 Déc 2010, 16:09
JeanJ a écrit:Dans le cas d'équation non-linéaire, une solution particulière ne sert pas à grand chose, pour ne pas aller jusqu'à dire que ça ne sert à rien (Peut-être pour une vérification à-postériori, lorsqu'on a trouvé la solution sans s'en servir ? )
Comme c'est une équation de ricatti si , une solution particulière sert.
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
 par JeanJ » 19 Déc 2010, 07:02
par JeanJ » 19 Déc 2010, 07:02
Comme c'est une équation de ricatti si , une solution particulière sert.
Ha! Encore cette vieille méthode qui oblige à trouver une solution particulière alors que ce n'est pas indispensable !
Voyez plutôt l'exemple de résolution de l'équation générale de Riccati (4) dans :
http://mathworld.wolfram.com/RiccatiDifferentialEquation.html
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
