Problème exrcice TS

par **thibaut47500** » 18 Déc 2010, 10:03

Bonjour à tous, voici l'énoncé sur lequel je bloque un peu:

La fonction

admet pour courbe représentative la courbe C ci-contre.

La droite d'équation

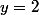
est asymptote à C en

. La courbe C admet une tangente horizontale au point A (-1;-2).

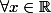
de l'intervalle

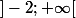
, on a :

avec

Grâce au graphique j'arrive à déterminer

et grâce à l'énoncé

. Ensuite je vois vaguement peut-être quelque chose avec les limites mais ce n'est pas très clair donc j'aimerais votre lumière. Merci d'avance

par **Euler07** » 18 Déc 2010, 10:20

Je suis pas sur que a,b,c appartiennent à R cube, il faut mettre des parenthèses pour désigner le triplet... Et que faut il faire en fait ?

par **thibaut47500** » 18 Déc 2010, 10:22

Oui tu as raison, je voulais dire a b et c des réels. En fait il faut déterminer a b et c.

par **Euler07** » 18 Déc 2010, 10:26

Tangente horizontal veut dire que la dérivée s'annule. T'as f'(-1)=0

par **thibaut47500** » 18 Déc 2010, 10:27

Ok mais ça ne veut pas dire aussi que f(-1)=-2?? Comment puis-je déterminer a b c à partir de ça?

par **Euler07** » 18 Déc 2010, 10:29

Si ta limite vaut 2 en +00 c'est que a vaut forcément 2.
Tu as

qui donne 2

par **thibaut47500** » 18 Déc 2010, 10:34

Pourriez vous développer un peu plus s'il vous plait je ne comprends pas la méthode?

par **Euler07** » 18 Déc 2010, 10:38

Quand tu développe ton dénominateur tu trouves x²+4x+4. Quand tu fais veux faire ta limite tu prends le monôme du plus au degré en haut et en bas, en simplifiant il reste a

Problème exrcice TS

Problème exrcice TS

Qui est en ligne