Borne supérieure
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 17 Déc 2010, 16:56
par GeorgeB » 17 Déc 2010, 16:56
Bonsoir , exercice difficile :
Montrer que
})
Une aide serait la bienvenue. Meric.
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 17 Déc 2010, 17:14
par kasmath » 17 Déc 2010, 17:14
GeorgeB a écrit:Bonsoir , exercice difficile :
Montrer que
})
Une aide serait la bienvenue. Meric.
il faut le faire par la caractérisation de
la borne sup
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 17 Déc 2010, 17:30
par GeorgeB » 17 Déc 2010, 17:30
J'imagine bien mais comment faire techniquement parlant ? Je n'arrive pas !
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 17 Déc 2010, 17:33
par girdav » 17 Déc 2010, 17:33
GeorgeB a écrit:Bonsoir , exercice difficile :
Montrer que
})
Une aide serait la bienvenue. Meric.
Bonjour,
qu'en est-il de la formule pour

réel?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 17 Déc 2010, 17:41
par arnaud32 » 17 Déc 2010, 17:41
et pour les complexes a partie imaginaire negative?
-
GeorgeB
- Membre Relatif
- Messages: 123
- Enregistré le: 15 Fév 2010, 20:21
-
 par GeorgeB » 17 Déc 2010, 17:50
par GeorgeB » 17 Déc 2010, 17:50
J'ai oublié de préciser que Im(z)>0 désolé.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Déc 2010, 18:07
par Ben314 » 17 Déc 2010, 18:07
Salut,
Normalement, pour une fonction de R dans R+ (par exemple la tienne !!!), le premier truc qui vient à l'esprit pour trouver le sup, c'est d'étudier les variations...
C'est pas toujours le plus malin (et ça marche pas toujours), mais ça a l'avantage (??) d'éviter de chercher des astuces...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Déc 2010, 18:12
par Nightmare » 17 Déc 2010, 18:12
Salut à tous !
On peut chercher du côté d'une preuve géométrique, R est une droite dont l'image par notre homographie est un cercle, reste à trouver le point sur celui-ci le plus éloigné de l'origine.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Déc 2010, 18:34
par Ben314 » 17 Déc 2010, 18:34
Nightmare a écrit:Salut à tous !
On peut chercher du côté d'une preuve géométrique, R est une droite dont l'image par notre homographie est un cercle, reste à trouver le point sur celui-ci le plus éloigné de l'origine.
C'est effectivement BEAUCOUP plus malin que l'étude de la fonction qui semble TRES gonflante...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Déc 2010, 18:57
par Nightmare » 17 Déc 2010, 18:57
Ben franchement j'ai essayé aussi en première idée, et même avec l'aide de Wolframalpha, je n'ai toujours pas eu le courage de terminer les calculs...
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 26 Déc 2010, 14:39
par cheria2010 » 26 Déc 2010, 14:39
salut messieurs
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 26 Déc 2010, 22:11
par cheria2010 » 26 Déc 2010, 22:11
salut
je trouve que :
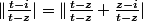
alors pour tout t de

on a:

le 2em membre atteint son max lorsque :
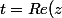)
donc :
}|)
ca ne suffit pas mais c'est pas mal .
-
cheria2010
- Membre Naturel
- Messages: 53
- Enregistré le: 14 Déc 2010, 13:55
-
 par cheria2010 » 28 Déc 2010, 20:32
par cheria2010 » 28 Déc 2010, 20:32
salut .
pas de nouveau :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités