Exercice : fonction 4/3-périodique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fac_m&m
- Messages: 9
- Enregistré le: 17 Oct 2010, 16:21
-
 par fac_m&m » 14 Déc 2010, 21:27
par fac_m&m » 14 Déc 2010, 21:27
Bonjour à tous ! Pourriez vous m'aider à faire l'exercice suivant ? Je ne sais vraiment pas quoi faire...
Soit
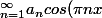)
une serie normalement convergeante sur R, et soit f sa fonction somme. Supposons que f est 4/3-périodique (périodique de période 4/3). Montrer que pour tout x appartenent à R,
=\bigsum_{n=1}^{\infty} a_{3n}cos(3{\pi}nx))
merci d'avance !
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 15 Déc 2010, 09:49
par arnaud32 » 15 Déc 2010, 09:49
comment ecris tu que ta fonction est 4/3 periodique? qu'en deduis tu pour les a_n etc ...
-
fac_m&m
- Messages: 9
- Enregistré le: 17 Oct 2010, 16:21
-
 par fac_m&m » 15 Déc 2010, 14:57
par fac_m&m » 15 Déc 2010, 14:57
Euh... je ne vois toujours pas le truc
j'ai bien
=\bigsum_{n=1}^{\infty} a_{n}cos(3{\pi}nx+{\pi}n(4/3)))
mais je ne vois pas quoi faire après pour montrer que les termes en

et
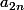
s'annulent. J'ai essayé plusieurs formules trigonométriques mais ça n'aboutit à rien...
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 15 Déc 2010, 15:09
par arnaud32 » 15 Déc 2010, 15:09
-
fac_m&m
- Messages: 9
- Enregistré le: 17 Oct 2010, 16:21
-
 par fac_m&m » 15 Déc 2010, 18:06
par fac_m&m » 15 Déc 2010, 18:06
Je me suis trompé (et toi aussi du coup) : en fait c'est
=f(x))
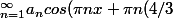)=\bigsum_{n=1}^{\infty} a_{n}cos({\pi}nx))
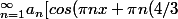)-cos({\pi}nx)]=0)
pour tout n et tout x
)-cos({\pi}nx)]=0)
mais sinon, ok je vois l'astuce ! j'avais pas du tout pensé à soustraire les deux sommes ! merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités