Je cherche la convergence ( quand n tend vers l'infini, pour tout t appartenant à R) de cette chose :
( exp(iat)*( 1-exp(ita(n+1)) ) ) / ( (n+1)*(1-exp(ita)) )
Où a=r+b+n r et b étant des constantes positives.
Si quelqu'un a une piste, j'en serais ravie :we:
Merci
Trouver une limite
5 messages
- Page 1 sur 1
C'est le 'i' des nombres complexes que tu as là ?
e^(io) = cos(o) + i*sin(o) est un nombre complexe (appelons-le z).
|z| est inférieur ou égal à 1.
a = r+b+n => a tend vers l'infini et a > n.
Essai de développer tes exponentiels et regarde si tu ne trouves pas une forme sympathique qui met en évidence la convergence.
e^(io) = cos(o) + i*sin(o) est un nombre complexe (appelons-le z).
|z| est inférieur ou égal à 1.
a = r+b+n => a tend vers l'infini et a > n.
Essai de développer tes exponentiels et regarde si tu ne trouves pas une forme sympathique qui met en évidence la convergence.
si exp(iat) est différent de 1, si t est fixé et qu'on fait varier n, ton truc est un truc borné divisé par (n+1) donc tend simplement vers 0.
Si exp(iat)=1, il fallait laisser ton truc sous la forme (exp(iat)+exp(2iat)+...+exp((n+1)iat))/(n+1) = (1+1+...+1)/(n+1) = 1.
ah ben j'avais pas fait gaffe que a dépend de n donc ça tombe à l'eau.
Si exp(iat)=1, il fallait laisser ton truc sous la forme (exp(iat)+exp(2iat)+...+exp((n+1)iat))/(n+1) = (1+1+...+1)/(n+1) = 1.
ah ben j'avais pas fait gaffe que a dépend de n donc ça tombe à l'eau.
ton probleme se ramene a trouver la limite de 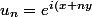}*\frac{ 1-(e^{i(x+ny)})^{n+1} }{ (n+1)(1-e^{i(x+ny)}) })
 est un sous groupe de
est un sous groupe de  qui est dense dans
qui est dense dans  ssi
ssi  \notin \mathbb{Q})
supposons que ce soit le cas
soit = e^{it})
=f(y\mathbb{Z}+2\pi \mathbb{Z})=f(\mathbb{R})=S^1)
tu peux donc extraire de})_n) une suite qui converge vers
une suite qui converge vers  et
et 
dans ce cas} | \leq \frac{2}{(n+1)(1-l)}) et
et } \rightarrow 0)
tu peux aussi extraire de})_n) une suite qui converge vers 1 telle que
une suite qui converge vers 1 telle que y)}-1|\leq (1/2)^{\phi (k) }) dans ce cas
dans ce cas } = \frac{e^{i(x+\phi (k)y)}}{\phi (k)+1}*\sum_{p=0}^{\phi (k)}e^{i(x+\phi (k)y)}^p)
et}-1| = |e^{i(x+\phi (k)y)}-1|+\frac{1}{\phi (k)+1}*|\sum_{p=0}^{\phi (k)}(e^{i(x+\phi (k)y)}^p-1) | \leq |e^{i(x+\phi (k)y)}-1|+\frac{|e^{i(x+\phi (k)y)}-1|}{\phi (k)+1} *\phi (k)(\phi (k)+1)/2*(1+1/2)^{\phi (k)})
}-1|\leq (1/2)^{\phi (k) }+\phi (k) /2*(3/4)^{\phi (k) }) et
et  } \rightarrow 1)
tu as donc au moins deux valeurs d'adherence pour ta suite et elle ne peut pas converger
si maintenant \in \mathbb{Q})

pour tout n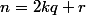 avec
avec  et
et }=e^{i(x+np/q\pi)}=e^{i(x+2kp\pi+rp/q\pi)}=e^{i(x+rp/q\pi)}) le suite des
le suite des })_n) n'a donc qu'au plus 2q valeurs d'adherence qui sont les
n'a donc qu'au plus 2q valeurs d'adherence qui sont les })
si toutes les suites extraites de u vont converger vers 0 et u converge vers 0
toutes les suites extraites de u vont converger vers 0 et u converge vers 0
sinon si toutes les suites extriates convergent vers 1, alors u converge vers 1; ce qui arrive si r=0,..,2q-1 ; et tu as alors pour=0 et r=1
r=0,..,2q-1 ; et tu as alors pour=0 et r=1 
ce qui te mene a p/q= 2k et donc et
et 
sinon la suite ne converge pas
supposons que ce soit le cas
soit
tu peux donc extraire de
dans ce cas
tu peux aussi extraire de
et
tu as donc au moins deux valeurs d'adherence pour ta suite et elle ne peut pas converger
si maintenant
pour tout n
si
sinon si toutes les suites extriates convergent vers 1, alors u converge vers 1; ce qui arrive si
ce qui te mene a p/q= 2k et donc
sinon la suite ne converge pas
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
