Accroissements finis
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 18:38
par hazaki » 07 Déc 2010, 18:38
edit failed
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Déc 2010, 18:41
par girdav » 07 Déc 2010, 18:41
Oui, ça marche avec les accroissements finis. Il te reste à encadrer la dérivée.
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 18:49
par hazaki » 07 Déc 2010, 18:49
edit failed
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Déc 2010, 19:03
par girdav » 07 Déc 2010, 19:03
On peut appliquer le fait "qu'il existe

tel que
-f(a) =f'(c)(b-a))
" avec

,

et
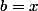
.
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 19:28
par hazaki » 07 Déc 2010, 19:28
edit failed
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Déc 2010, 19:29
par girdav » 07 Déc 2010, 19:29
On l'applique plutôt à
=\ln(1+x))
.
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 19:30
par hazaki » 07 Déc 2010, 19:30
edit failed
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 19:33
par hazaki » 07 Déc 2010, 19:33
edit failed
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 07 Déc 2010, 19:58
par girdav » 07 Déc 2010, 19:58
J'ai enlevé la faute de frappe : je voulais bien sûr dire
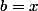
.
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 20:05
par hazaki » 07 Déc 2010, 20:05
edit failed
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 07 Déc 2010, 20:15
par bentaarito » 07 Déc 2010, 20:15
hazaki a écrit:ok j'ai donc x*f'(c)=ln(x+1)
donc ça donne 0 < ln(x+1)/x < 1 ?
Non pas 0 c'est
=.... \in ].,.[)
) :hum: :hum:
-
hazaki
- Membre Naturel
- Messages: 70
- Enregistré le: 05 Oct 2010, 20:31
-
 par hazaki » 07 Déc 2010, 20:19
par hazaki » 07 Déc 2010, 20:19
edit failed
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
