Developpement limité?

[Fed]

Bonjour,

Il s'agit d'établir |1-x²/2-cosx|<= x^4/24 sur [0,pi/2]

j'ai pensé à comparer |-cosx| au DL à l'ordre 4 de cos(x) mais je ne suis pas sûr que je puisse extraire la fonction 1-x²/2 aussi facilement de la valeur absolue du terme de gauche...

[Sylviel]

Le DL ne te donneras jamais d'estimation sur un intervalle, juste en un point. En revanche il existe une formule de Taylor Lagrange qui te donne ce genre d'estimation... Sinon à la main ! (étude de fonction...)

[Fed]

Bonjour,

J'ai un exo qui me demande de calculer le D.L d'un quotient de fonctions, donc le quotient du DL de ces fonctions si j'ai bien compris.
Mon cours n'évoquant pas les differentes méthodes dont la division par puissances croissantes des polynômes, je suis perdu dans mon exercice, et j'aimerais beaucoup que l'on m'explique (mieux que wikipedia) ce procédé.

Merci

[bentaarito]

Bonsoir,
pour développer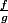 à l'ordre n, on développe g à l'ordre n et suivant la valuation p de DL obtenu on développe f à l'ordre n+p
J'espère que je réponds à ta question (et que tu n'est pas entrain de demander la technique de la division suivant les puissances croissantes)
Je suis prêt à te donner des exemples :lol3:

[Sasumax]

En remarquant que pour tout x on a |sin x|<=|x|, on ecrit pour x dans [0, pi/2] que |sin x|<= x soit -x <= sin x <= x, ou encore -t <= sin t <= t ;pour t appartenant au même intervalle
En integrant de 0 à x, on obtient -(x^2)/2 <= 1 - cos x <= (x^2)/2. En integrant encore 2 fois, on obtient -(x^4)/(2*3*4) <= (x^2)/2 + cos x - 1 <= (x^4)/(2*3*4) , ce qui donne
|(x^2)/2 + cos x - 1 | <= (x^4)/24, soit |1 - (x^2)/2 - cos x | <= (x^4)/24, car |x| = |-x|

Il faut aussi noter que les developpements limités ne sont valides qu' au voisinage d'un nombre, et non sur tout intervalle. En fait, pour que le reste o(x^4) puisse être petit, x doit être très proche de 0
ce qui veut dire que l'intervalle tenant lieu de voisinage doit être très peti, par exemple, ]-e, e[, avec e trés petit.

Bonne journée. :lol3: