Bonjour,
voilà un petit exercice de TD :
Soit f = R->R défini par f(x)=x*E(1/x) et 1 si x=0.
Déterminer l'ensemble des points de continuité de f;
Donc j'ai trouvé que f est continue sur ]-inf;-1[, ]1;+inf[ et sur ]-1;1[ privé des valeurs de x telles que 1/x appartient à Z.
Cependant j'ai un peu du mal à expliquer les résultats entre -1 et 1.
Merci de bien vouloir éclaircir mon problème
Continuité de x*E(1/x)
5 messages
- Page 1 sur 1
E est continue sur R\Z
sur ]-inf;-1[ et ]1;+inf[ la fonction inv: x ->1/x est continue et inv(]-inf;-1[ U ]1;+inf[) est ]-1,0[U]0,1[ ensenble sur lequel E est continue donc f est continue sur ]-inf;-1[ U ]1;+inf[
en -1 et 1 f n'est pas continue car les limites a gauche et a droite sont differentes.
sur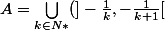\cup \bigcup_{k \in N*}(]\frac{1}{k+1},\frac{1}{k}[)) inv est continue et l'image de cet ensemble est (]-inf;-1[ U ]1;+inf[)\Z ensenble sur lequel E est continue donc f est sur A
inv est continue et l'image de cet ensemble est (]-inf;-1[ U ]1;+inf[)\Z ensenble sur lequel E est continue donc f est sur A
en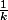 pour k entier positif non nul f n'est pas cintinue car les limites a droite et a gauche sont differentes.
pour k entier positif non nul f n'est pas cintinue car les limites a droite et a gauche sont differentes.
reste la cas de zero qui n'est pas un moint de cotinuite car la suite des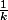 tends vers mais la suite image vers +inf
tends vers mais la suite image vers +inf
sur ]-inf;-1[ et ]1;+inf[ la fonction inv: x ->1/x est continue et inv(]-inf;-1[ U ]1;+inf[) est ]-1,0[U]0,1[ ensenble sur lequel E est continue donc f est continue sur ]-inf;-1[ U ]1;+inf[
en -1 et 1 f n'est pas continue car les limites a gauche et a droite sont differentes.
sur
en
reste la cas de zero qui n'est pas un moint de cotinuite car la suite des
parce que j'ai remarqué que soit 1/x appartenant à Z, pour tout z appartenant à [-1;1],
si z appartient à ]1/x;1/(x+1)[, z=z*E(1/x)=z*x,
donc si z<0 : z décroit de 1+x à 1;
si z>0 : z croit de 1 à 1+x;
or x*E(x)=1 pour 1/x appartenant à Z et x compris entre -1 et 1
donc il y a discontinuité en tout point x tq 1/x appartient à Z.
non ?
si z appartient à ]1/x;1/(x+1)[, z=z*E(1/x)=z*x,
donc si z<0 : z décroit de 1+x à 1;
si z>0 : z croit de 1 à 1+x;
or x*E(x)=1 pour 1/x appartenant à Z et x compris entre -1 et 1
donc il y a discontinuité en tout point x tq 1/x appartient à Z.
non ?
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
