Les suites arithmétiques et géométrique

[levisionniste]

bonjour à tous,

je viens vous trouver car je suis bloquer dans un devoir côté sur les suites arithmétique et géométrique...

notre professeur nous a donner 5 questions à rendre demain j'ai tenter de les résoudre mais je suis à présent perdu


voici les formules dont nous disposons

suite arithmétique :

Tn = T1 + ( n - 1 ) * R

Sn = ((Tn + T1 ) * n ) / 2

suite géométrique :

Tn = T1 * q^(n-1)

Sn = T1 * ( ( q^(n) -1 ) / ( q -1 ) )

Pn = racine ² de ( ( T1 * Tn ) ^ n )


voici le questionnaire :



Un cycliste descend une colline en parcourant 1,2 m durant la première seconde . il roule de plus en plus vite : chaque seconde il parcoure 1,5 m de plus que la seconde précédente. Sachant que le cycliste atteint le bas de la colline en 11 secondes , calculer la distance totale parcourue

Donné :

T1 = 1,2
R = 1,5
n = 11

Formule :

Tn = T1 + ( n – 1 ) * R

Sn = ((Tn + T1) *n) /2

Résolution

Tn = 1,2 + (11-1)* 1,5

Tn = 16,2

S11= ((16,2+1,2)*11)/2

S11 = 95,7


2) on donne T10 = 10 et T 1000 = 100000 d’une suite arithmétique. Calculer S100

résolution :

r = 101

T1= -899


3) détermine 3 nombres formant une suite géométrique dont la somme vaut 21 et le produit vaut –729


4) déterminer 4 nombres formant une suite géométrique dont la somme des deux premier terme vaut 20 et la somme des deux dernier termes est égale à 320


mise à part les deux premier je n'ai su faire les autre, aidez moi s'il vous plait

[Sh0nty]

Bonsoir levisionniste,

Pour la 3), trois nombres , et 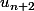forment une suite géométrique si et seulement si :
et avec q la raison de la suite.
Tu peux donc exprimer la somme de ces trois nombres :

Or comme est la somme de trois termes d'une suite géométrique de premier terme 1 et de raison q, on a pour :

Donc (1)

De plus, leur produit vaut -729 donc :

D'où (2)

Il ne te reste plus qu'à résoudre ce système de deux équations à deux inconnues!

En espérant t'avoir aidé,
Sh0nty

[levisionniste]

j'ai trouver q =-4 et T1 donc a (21/13) mais je ne trouve pas le numéro 4 et j'ai tres dur a comprendre votre écriture scientifique

[Sh0nty]

Qu'est-ce que tu n'as pas compris?

Sh0nty

[levisionniste]

j'ai l'impression que vous avez changer les lettres néanmoins ce n'est pas mon problème mais bien l'exercices numéro 4

[levisionniste]

pour le numéro 4 , T1 +T2 = 20
T3 + T4 = 320

donc S = 340 et n = 4 mais je n'arrive pas a aller plus loin

[Sh0nty]

Le truc c'est de bien décomposer l'énoncé :

3 nombres formant une suite géométrique

Soient T1, T2 et T3 trois nombres formant une suite géométrique. Comment cela se traduit-il? Comme ceci :
Soit q la raison de cette suite géométrique.
On a donc T2 = qT1 et T3 = qT2 = q²T1 d'après la définition de la suite géométrique.

dont la somme vaut 21

On a alors T1 + T2 + T3 = 21.

suite géométrique : Sn = T1 * ( ( q^(n) -1 ) / ( q -1 ) )

Ici le nombre de terme est 3, donc n = 3 dans l'égalité précédente. On en déduit que :
(1)

le produit vaut –729

Donc T1xT2xT3 = -729
D'après les égalités au début de mon post, il vient que :

D'où (2)

Il faut ensuite résoudre le système composé des équations (1) et (2).

Sh0nty

[levisionniste]

oui je ai compris l'exercice 3 mais je n'arrive pas a faire l'excercice 4

déterminer 4 nombres formant une suite géométrique dont la somme des deux premier terme vaut 20 et la somme des deux dernier termes est égale à 320

[Sh0nty]

Pour l'exercice 4, on a :

4 nombres formant une suite géométrique

Soient T1, T2, T3 et T4 ces nombres.
Ils forment une suite géométrique, de raison q, donc :
T2 = qT1, T3 = q²T1 et

la somme des deux premier terme vaut 20

T1 + T2 = 20 donc T1 + qT1 = 20 soit T1(q+1) = 20 (1)

la somme des deux dernier termes est égale à 320

T3 + T4 = 320 donc soit q²T1(q + 1) = 320 (2)

Il ne te reste plus quà résoudre le système composé des équations (1) et (2).

Sh0nty

[levisionniste]

je n'arrive pas a subbstituer

[Sh0nty]

Comme T1(q+1) = 20, substitue T1(q+1) dans la seconde équation par 20, ce qui donne 20q² = 320.

Sh0nty

[levisionniste]

donc q= 5 et T1 = 4 ??

[levisionniste]

l'inverse pardon

[levisionniste]

pardon je me suis complêtement tromper

j'ai trouver cette fois

q = -4 et T1 = -20/3

[Sh0nty]

Il a deux solutions à l'équation : q = 4 ou q = -4.
Dans le premier cas tu obtiens : T1(4+1) = 20 soit T1 = 4.
Dans le second cas tu obtiens : T1(-4+1) = 20 soit

Sh0nty