Primitive/dérivée

par **Mr.DDR** » 24 Nov 2010, 17:48

Bonjour tout le monde, alors jais une dérivée à faire :

Quand il y a sqrt{x} on applique la formule :

Mais comme il y a un x devant, sa donne quoi ?

merci

par **Arnaud-29-31** » 24 Nov 2010, 17:51

Salut,

Bien sur que non ... la dérivé de k.u vaut k.u' si k est une constante !

La il faut appliquer la formule de dérivation d'un produit.

par **Sh0nty** » 24 Nov 2010, 17:53

Bonjour Mr.DDR,

Tu as ici un produit de deux fonctions :

et

La formule de la dérivée d'un produit de fonction est :

Il ne te reste plus qu'à calculer

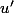
et

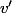
En espérant t'avoir aidé,
Sh0nty

par **Mr.DDR** » 24 Nov 2010, 18:22

ha merci sh0nty et Arnaud-29-31

donc sa me donne:

ensuite il faut déduire de la première question une primitive de

là j'ais aucune idée

par **Arnaud-29-31** » 24 Nov 2010, 18:40

Bein tu as

et on te demande une primitive de

... franchement tu ne peux pas avoir aucune idée là ...

par **Mr.DDR** » 24 Nov 2010, 18:48

je l'avais pas vu sous cette forme ^^ mais je vois pas ce que me donne la primitive de

par **Arnaud-29-31** » 24 Nov 2010, 18:51

Si

, on peut aussi écrire que

...

par **Mr.DDR** » 24 Nov 2010, 18:58

donc la primitive c'est ça puisque c'est égale à la dérivé

non ?

par **Sylviel** » 24 Nov 2010, 19:05

donc la primitive c'est ça

mais encore ?

par **Arnaud-29-31** » 24 Nov 2010, 19:05

Ca veut pas dire grand chose ce que tu viens de dire mais je suppose que tu as compris.

par **Sh0nty** » 24 Nov 2010, 19:07

donc la primitive

Il ne faut pas dire la primitive mais une primitive.
Tu as donc trouvé une primitive de

qui est

Donc les primitives de

sont les fonctions de la forme

Sh0nty

par **Mr.DDR** » 24 Nov 2010, 20:12

^^ d'un coté tu ma compris.

merci bien :)