Calcul d'un exposant

[levisionniste]

bonsoir,


hier soir en m'endormant , je me suis poser une question...

comment calculer un exposant si celui si est l'inconnu ?


et bien je n'ai pas trouver de réponse alors je me demande à présent si vous
pourriez m'aider s'il vous plait ?


exemple 2^(3)= 8 et l'inconnue est l'exposant en 3 2^(x) = 8

[Rebelle_]

B'soir

Penses-tu aux fonctions puissances avec un réel (je ne sais pas faire la flèche avec une barre à droite ) ?
Si oui, la fonction est définie sur R+ privé de 0 telle que pour tout réel.

[levisionniste]

je ne comprend pas bien ce que vous me dite

pourriez vous l'illustrer avec l'exemple de 2³ = 8 s'il vous plait

donc je cherche l'exposant , la puissance en d'autre terme

[Arnaud-29-31]

Salut,

Ton problème revient donc à déterminer x lorsque l'on te dit .
Il existe tout simplement une fonction réciproque à la fonction (de même que la fonction racine carrée est la fonction réciproque de )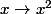
Il s'agit de la fonction, étant nommée fonction logarithme de base a.

Donc si

Pour ton exemple, donc

Tu trouveras sur ta calculatrice le log de base 10 noté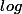 et le log de base e (car très utilisé en math : c'est le logarithme néperien) noté ...
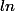Je n'ai pas envie de t'embrouiller avec des choses que tu auras le temps de voir plus tard mais comme je suppose que tu vas vouloir vérifier le calcul, je te donne la formule suivante : donc ton x ici vaut

[Rebelle_]

Donc si tu parles des fonctions puissances entières c'est plus simple.

Soit x un réel et n un entier naturel. On distingue les cas des puissances positives et des puissances négatives.

Pour les puissances positives, par convention on pose pour tout x réel, x^0 = 1 et x^n = x*x*...*x (n fois) si n est supérieur ou égal à 1.

Pour les puissances négatives, on pose x^(-n) = 1/x^n. Bien sûr, dans ce cas la fonction est définie sur R* et non sur R.

Il y a de nombreuses règles de calcul ensuite... :)